Capitolo 4 Le basi
4.1 Che cosa è l’ambiente R
R è un ambiente di programmazione. Parafrasando Morpheus che sfida Neo nella palestra virtuale di “Struttura”, diremo che l’ambiente R ha le sue regole, e che conoscerle rappresenta il primo passo per impadronirsi di questo strumento (e aggirare o infrangere le sue regole).
In questa sezione saranno introdotte alcune nozioni generali che, spesso, sono date per scontate e quindi non chiaramente delineate. Nella nostra esperienza, dare per scontati questi concetti rende ostica il primo impatto con R e le prime fasi del suo utilizzo, cioè quelle durante le quali i nuovi utenti devono assimilare la sintassi, le diverse tipologie di dati e le strutture all’interno delle quali possono essere organizzati e gestiti. Come tutti gli ambienti e i linguaggi di programmazione, R ha una sua sintassi e, sebbene essa non sia particolarmente complessa e articolata, sicuramente rappresenta il primo grande ostacolo a un utilizzo rapido ed efficace.
Al contrario, se resi comprensibili e chiari, i capisaldi della sintassi possono essere dei punti di riferimento quando guardiamo un codice scritto da altri o da noi stessi un pò di tempo fa… E dunque la prima parte di questo manuale è concepita per illustrare le regole generali che sono alla base delle procedure nell’ambiente R.
Dunque impareremo la differenza sostanziale tra una espressione ed una assegnazione, l’utilizzo delle parentesi e le diverse tipologie di oggetti di base.
Successivamente, imparemo a comporre dei semplici codici combinandoi espressioni, assegnazioni, e oggetti. Nel farlo, cercheremo subito di introdurre delle norme di stile e delle buone pratiche che ci aiuteranno a essere più ordinati, efficienti ed efficaci.
R è un ambiente per Object-oriented programming, cioè uno stile di programmazione diventato molto popolare negli ultimi anni. Questo stile si basa sull’utilizzo (la manipolazione mediante comandi) di oggetti, un approccio che rende molto semplice accedere (leggere e scrivere) ai dati in memoria e combinarli in strutture che possono essere anche molto complesse. Aspetti fondamentali dei lunguaggi object-oriented sono il concetto di classe e quello di metodo, sui quali torneremo in seguito in maniera approfondita.
Classi e Metodi sono legati dal fatto che, in R, la computazione si basa sull’applicazione di specifici metodi a oggetti di specifiche classi. Non esiste una corrispondenza biunivoca tra classi e metodi, piuttosto molti metodi possono essere applicati a oggetti di classi diverse e viceversa. Tuttavia, metodi diversi sono generalmente specializzati per essere applicati su specifiche classi di oggetti. Questa associazione metodi-classi è spesso molto intuitiva, ma esistono funzioni generiche per determinare di che classe sia un dato oggetto e quali siano i metodi su di esso applicabili.
Un altro aspetto importante dei lunguaggi object-oriented è quello di inheritance (eredità). Questo aspetto può essere sintetizzato come la capacità degli oggetti generati durante l’esecuzione di un codice o di una procedura di calcolo di “portarsi appresso” le caratteristiche degli oggetti “genitori” o delle funzioni “genitrici”, cioè quelli a partire dai quali sono stati generati. Un esempio intuitivo è il seguente: se definisco due quantità numeriche a e b e le sommo, quello che ottengo (c) erediterà le caratteristiche dei genitori (numerici entrambi) e potrà essere trattato come tale. Questo aspetto semplifica enormemente il lavoro poichè, a differenza di quanto avviene in linguaggi di base, non è necessario pre-definire l’oggetto c indicandone esplicitamente le caratteristiche e poi riempirlo.
Continuando l’elenco dei grandi vantaggi di R, dobbiamo sicuramente menzionare la sua enorme Community. Secondo la compagnia di analisi del software TIOBE, l’ambiente R è attualemnte al 9° posto tra i linguaggi più popolari ma, soprattutto, è quello che continua a crescere al ritmo più sostenuto.
TIOBE <- data.frame(Name = c("C", "Java", "Python", "C++", "C#", "Visual Basic", "Java Script", "R",
"PHP", "SQL", "Go", "Swift", "Pearl", "Assembly language", "Ruby",
"MATLAB", "Classic Visual Basic", "Groovy", "Objective-C", "Rust"),
Ratings = c(16.98, 14.43, 9.69, 6.84, 4.68, 4.66, 2.87, 2.79, 2.24, 1.46, 1.43, 1.42, 1.11, 1.04, 1.03, 0.86, 0.82, 0.77, 0.76, 0.74),
Change = c(1.83, -1.60, -0.33, 0.78, 0.83, 0.97, 0.62, 1.97, 0.17, -0.17, 0.45, 0.53, 0.25, -0.07, -0.28, -0.41, -0.20, -0.46, -0.93, 0.29))
knitr::kable(
head(TIOBE, nrow(TIOBE)), caption = 'TIOBE Index for August 2020',
booktabs = TRUE
)| Name | Ratings | Change |
|---|---|---|
| C | 16.98 | 1.83 |
| Java | 14.43 | -1.60 |
| Python | 9.69 | -0.33 |
| C++ | 6.84 | 0.78 |
| C# | 4.68 | 0.83 |
| Visual Basic | 4.66 | 0.97 |
| Java Script | 2.87 | 0.62 |
| R | 2.79 | 1.97 |
| PHP | 2.24 | 0.17 |
| SQL | 1.46 | -0.17 |
| Go | 1.43 | 0.45 |
| Swift | 1.42 | 0.53 |
| Pearl | 1.11 | 0.25 |
| Assembly language | 1.04 | -0.07 |
| Ruby | 1.03 | -0.28 |
| MATLAB | 0.86 | -0.41 |
| Classic Visual Basic | 0.82 | -0.20 |
| Groovy | 0.77 | -0.46 |
| Objective-C | 0.76 | -0.93 |
| Rust | 0.74 | 0.29 |
par(las = 2, mar = c(5,10,1,1), cex = 0.7)
barplot(TIOBE$Ratings[order(TIOBE$Ratings, decreasing = F)],
names.arg = TIOBE$Name[order(TIOBE$Ratings, decreasing = F)],
xlab = "Ratings (%)", ylab = "",
col = c(rep("grey",12),"blue",rep("grey",7)), horiz = T)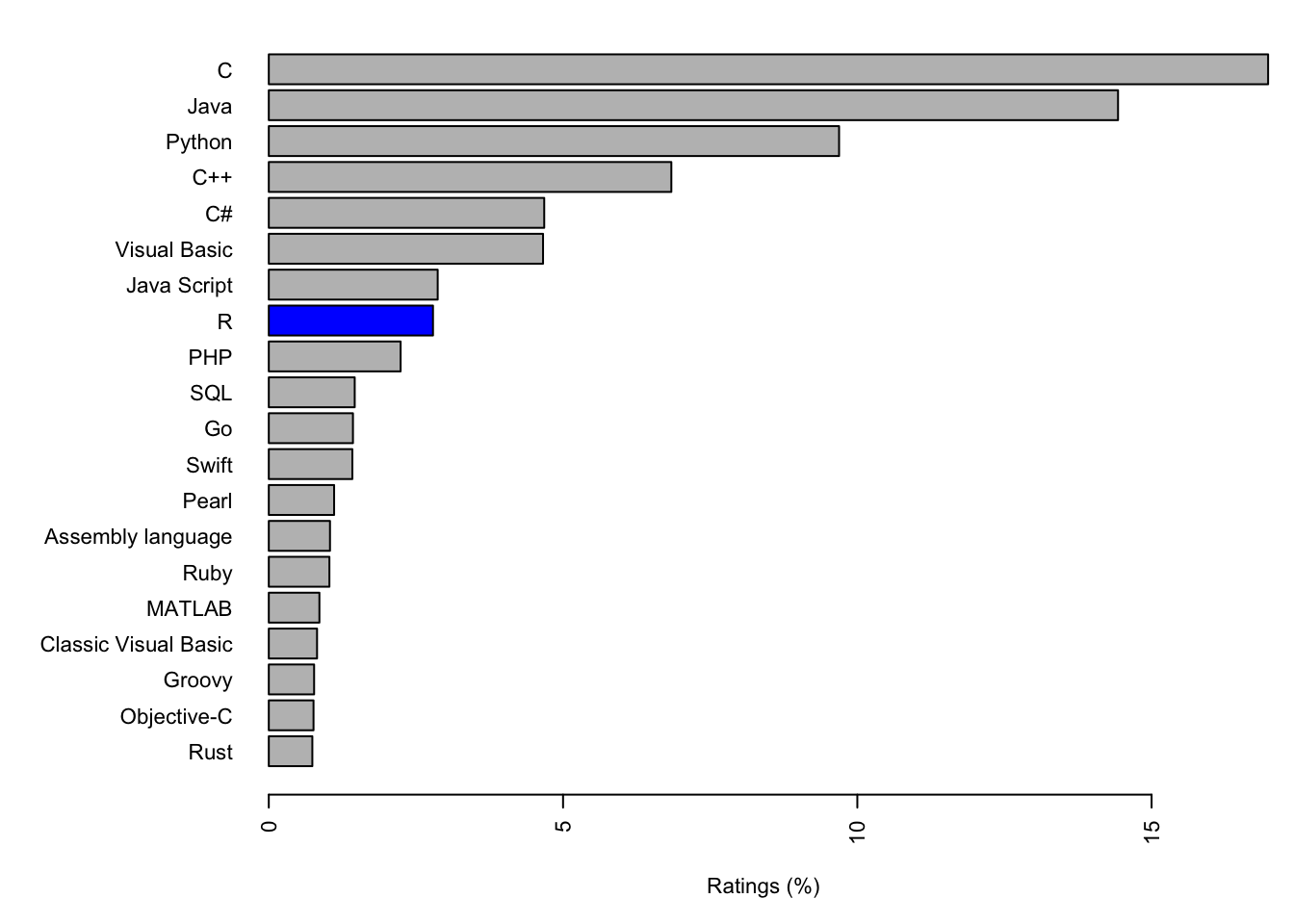
Questo dato è ancora più significativo se si considera che R non è esattamente un ambiente per produrre software compilato e quindi eseguibile (come avviene invece con i membri della famiglia C). Perchè questo aspetto è così importante? Semplicemente perchè, essendo R un ambiente “libero”, ogni utente può attingere a una sterminata banca dati di informazioni, algoritmi, pacchetti aggiuntivi e funzioni già sviluppate da altri utenti… e spesso può contare sull’aiuto diretto di una vasta community. In ambito scientifico, R ha avuto (e continua ad avere) una diffusione inarrestabile perchè incarna perfettamente alcuni ideali della ricerca: la possibilità di sviluppare metodologie completamente replicabili, chiare e ulteriormente implementabili. Come ha giustamente argomentato qui Shannon Ellis, una community ampia offre sviluppatori, esperti, potenziali collaboratori, estensori di documentazione, persone che mettono alla prova le nostre routine, “agitatori” (che sono sempre utili per tenere viva la community!) o semplicemente persone gentili che sono disposte ad aiutare i neofiti. Ma, soprattutto, qualsiasi sia la sfida con la quale siete alle prese, molto probabilmente qualcuno ci si è già cimentato e potrete ripartire dal suo lavoro. Non è forse, questo, un enorme vantaggio? Shannon Ellis ha compilato una lista di siti/blog che rappresentano i principali canali web della community di R. I principali sono:
- (Revolution) Local R meetup groups - un motore di ricerca che aiuta a trovare riferimenti nella propria area di interesse (per salire sulla spalle dei giganti);
- Rweekly - un magazine settimanale di quello che succede nel mondo di R;
- R-bloggers - un archivio di post utili fatti tra utenti di R;
- Stack Overflow - dove cercare risposte alle nostre domande, spesso legate alle difficoltà dei neofiti (ma non solo)
Una bella e completa descrizione di cosa sia R la trovate qui. In sintesi:
- R è un ambiente integrato e coerente per l’analisi statistica;
- R è contemporaneamente un linguaggio ed un software;
- R è un potente strumento per la produzione di grafici (originali);
- R è distribuito gratuitamente sotto i vincoli della GPL - General Public License ed è disponibile per diverse architetture hardware e sistemi operativi: Unix, Linux, Windows, MacOS.
- R è disponibile presso il sito The R Project for Statistical Computing dove è possibile scaricare, oltre che il programma base, anche una serie di moduli aggiuntivi e un’ampia manualistica (in lingua inglese) sull’ambiente che va dall’installazione del software al suo utilizzo nell’analisi dei dati;
- il sorgente di R è scritto parte nel linguaggio C e parte nel linguaggio Fortran.
4.2 A cosa serve/non serve R
R non è una panacea, e anche gli appassionati di questo strumento devono essere a conoscenza dei suoi difetti quanto dei suoi pregi. Da una parte, R si comporta come gli smartphone (un nuovo tipo di device che, dalla sua comparsa sul mercato, ha completamente “assorbito” e messo fuori dal mercato altri device come i lettori mp3, le fotocamere, i navigatori satellitari). Infatti chi usa R può facilmente rinunciare a fogli di calcolo, software proprietari per la statistica, gestori di database, piattaforme per la geostatistica, software per l’analisi e la manipolazione di immagini, e la lista potrebbe continuare. R può servire praticamente a tutto! Un altro grande vantaggio di R è che, essendo un software opensource, si può accedere al codice sorgente e modificarlo. R è del tutto gratuito. R possiede un’ampia biblioteca di manuali e dispense accessibili gratuitamente in rete, oltre a pubblicazioni a pagamento. L’installazione base di R può essere integrata con librerie di funzioni addizionali (il vero valore aggiunto per il mondo della ricerca) che ne ampliano a dismisura le capacità. R offre un supporto tramite l’R Development Core Team. Infine, R sa “parlare” con altri linguaggi, da C a SQL a fortran e Python, per cui si possono integrare metodi e funzioni sviluppate in altri contesti. Per essere proprio completi, è importante ricordare che.
- R ha una quantità veramente incredibile di funzioni grafiche che consentono di ottenere grafici estremamente efficaci dal punto di vista scientifico ma anche “belli”
- R permette di essere creativi ed efficienti, poichè consente di scrivere nuove funzioni o intere librerie in maniera molto semplice
- La sua versione base è molto snella, ed essendo sviluppato secondo una logica vettoriale lavora molto bene su vettori e matrici
E le brutte notizie?
Beh…
- R è “brutto”: la sua interfaccia non è pensata per essere bella e accattivante come gli OS ai quali siamo abituati. L’interfaccia utente a carattere (CUI) di R è anche “ostico”, poichè ci costringe a cambiare modo di lavorare. E’ vero che è presente anche un’interfaccia GUI (Graphical User Interface), ma gli utenti esperti non la usano quasi mai;
- R è “un elefante”: può arrivare a occupare una grande quantità di memoria e la sua velocità di calcolo è di gran lunga inferiore a quelle di ambienti e linguacci di livello più basso (come la famiglia C o Visual Basic). Questo, a volte, costringe gli utenti più esperti a compilare delle funzioni in C tutte le volte che le loro analisi diventano computational and time demanding;
- Non tutte le funzioni di R sono ottimizzate per avere elevate prestazioni (un buon esempio sono le funzioni di ottimizzazione numerica). A volte sarete costretti a metterci del vostro per sviluppare funzioni nuove o più performanti;
- Se sviluppate un’applicazione basata su R, è vostro onere tutto quello che rigarda il debug e il mantenimento: se salta fuori un problema, non potete prendervela con nessun altro!
4.3 “What You See Is What You Mean”: dallo Script al terminale (e viceversa)
Per affrontare la prima parte, dedicata a una carrellata degli aspetti base (concettuali e di sintassi) dell’ambiente R, è necessario assimilare alcuni termini (e strumenti): Il terminale (detto console in inglese, così come è denominata la sua finestra nell’interfaccia di R studio), è l’ interfaccia attraverso il quale l’utente interagisce con R.
Fonte: https://xkcd.com/149/
Citando testualmente Wikipedia: “In informatica una interfaccia a riga di comando[1] (dall’inglese command line interface, in acronimo CLI) o anche console, a volte detta semplicemente riga di comando e, impropriamente[senza fonte], prompt dei comandi, è un tipo di interfaccia utente caratterizzata da un’interazione testuale tra utente ed elaboratore (vedi shell): l’utente impartisce comandi testuali in input mediante tastiera alfanumerica e riceve risposte testuali in output dall’elaboratore mediante display o stampante alfanumerici. Nei sistemi operativi moderni usati nei personal computer, al posto della CLI, in buona parte, c’è l’interfaccia grafica con caratteristiche tipicamente user friendly”. Il primo (e forse principale) trauma al quale il neofita di R si trova di fronte è la necessità di rinunciare (possibilmente da subito e definitavamente) all’interazione tramite il mouse e quindi le interfacce a finestre e menù a tendina che tanto ci sono familiari e rispetto alle quali abbiamo sviluppato una certa dipendenza! Quando si comincia a usare R, bisogna accettare di inserire i comandi digitandoli direttamente nel terminale o predisponendoli in uno script (una sequenza di comandi annotata da qualche parte, generalmente in un editor di testo o in una apposita finestra di R studio). Ci sono due motivi principali per questo: 1. Sarebbe impossibile codificare tutti i possibili comandi di R in un menù grafico o a tendina, senza considerare che questo limiterebbe comunque l’originalità degli utenti e renderebbe assai complesso combinare insieme varie funzioni; 2. Imparare a usare il terminale rende il lavoro estremamente più veloce (provare per credere). Questo secondo aspetto accomuna R a tanti altri ambienti di alto livello e persino a sistemi operativi come Ubuntu e Debian (due delle principali distribuzioni di Linux). Per utilizzare il terminale, però, non basta conoscere la sintassi dei comandi: bisogna cambiare filosofia. Quando utilizziamo un elaboratore di testo, digitiamo i caratteri sapendo che esiste una precisa corrispondenza tra i tasti che premiamo e il risultato che apparirà sullo schermo. Questo modo di operare viene denominaro What You See Is What You Get (“quello che vedi è quello che è” o “ottieni quanto vedi” - acronimo WYSIWYG). Utilizzare il terminale di un ambiente come R significa invece applicare la filosofia What You See Is What You Mean (letteralmente: quel che vedi è ciò che intendi; sinteticamente, vedi quanto intendi - acronimo WYSIWYM). In sostanza, le istruzioni che digitiamo non sono semplici parole sullo schermo ma implicano l’applicazione di funzioni anche complesse che, nelle intenzioni dell’utente, devono restituire un risultato di qualche tipo. L’utilizzo di R si svolge tipicamente attraverso un continuo passaggio dall’editor di testo, dove si modica lo script, al terminale dove lo si esegue. Se poi si usano interfacce avanzate come R studioTIOBE, si può disporre di utili finestre accessorie (come quella dei grafici). La figura seguente ci mostra una tipica schermata di R studio
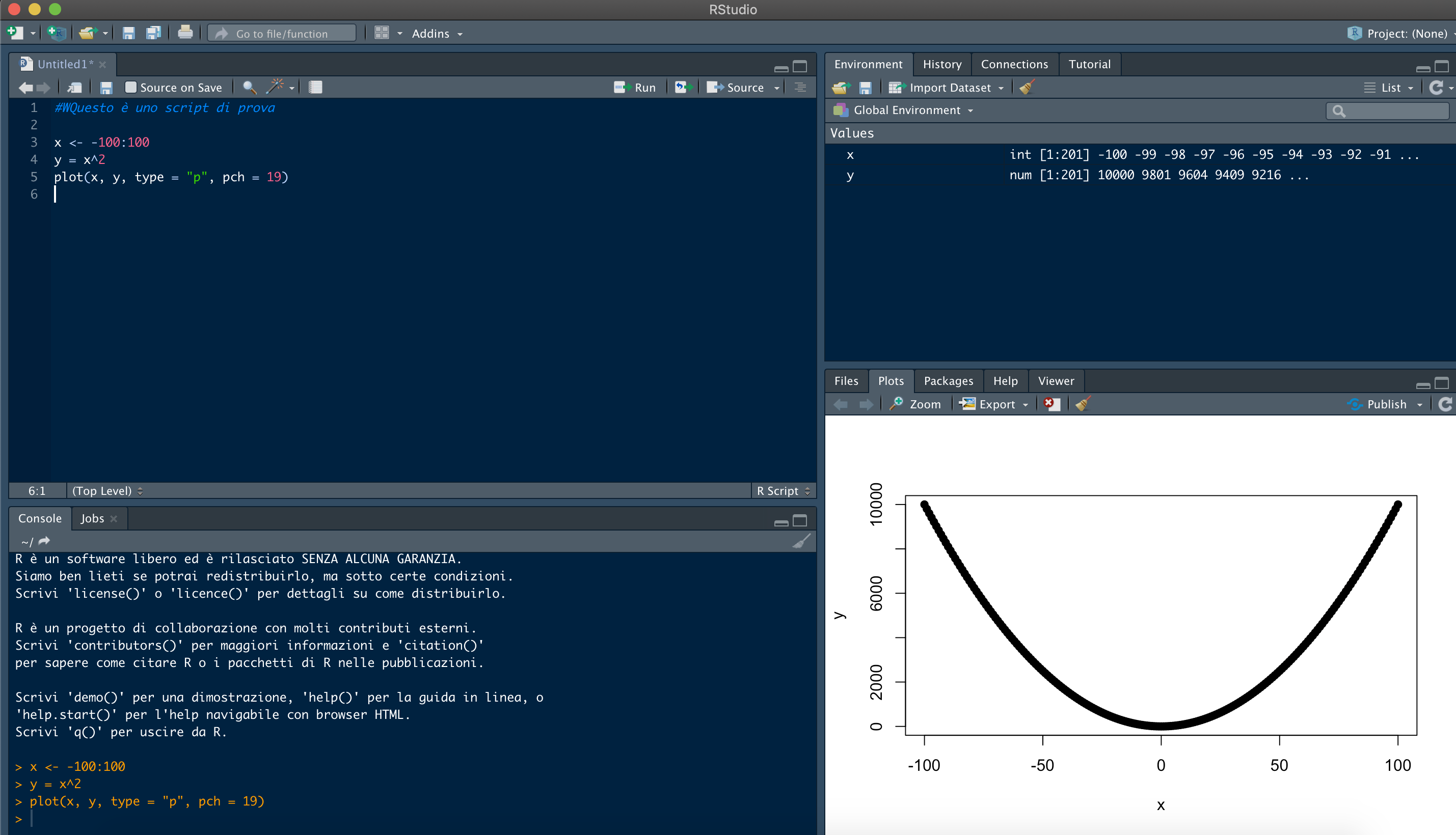
Un’anteprima dell’interfaccia di R studio
L’interfaccia di Rstudio contiene 4 finestre che sono spesso organizzate in questo modo (ma l’utente ha ampie possibilità di personalizzarle). Analizziamo questo esempio:
In alto a sinistra c’è lo Script o gli Script se si vuole gestire più procedure separate. Questa finestra è semplicemente un blocco note multipagina che consente di inviare i comandi direttamente al terminale
In basso a sinistra ecco proprio lui, il terminale, ovvero il canale di collegamento in ingresso da noi verso R. In Rstudio, questa finestra si chiama Console. Avete presente Ellen Ripley che comunica con Mother, il super computer cattivo dell’astronale Nostromo, mediante un terminale? Ecco, il concetto è quello e… a volte penserete che R è antipatico quasi quanto Mother :-)
In alto a destra c’è una finestra “composita” che racchiude Environment, all’interno del quale troveremo un elenco (con alcune caratteristiche essenziali) degli oggetti nella memoria della sessione, History, una cronologia dei comandi passati alla Console, e infine le tre sottofinestre Connections, Build e Tutorial sulle quali, per ora, possiamo sorvolare.
In basso a destra c’è un’altra finestra “composita” che racchiude Files, cioè l’elenco dei file nella cartella di lavoro (la directory del pc) scelta per la sessione, Plots, che conterrà le anteprime dei grafici realizzati, Packages, che è un prontuario di tutti gli help dei pacchetti installlati, Help, l’interfaccia minimale di aiuto che presto impareremo ad apprezzare, e Viewer, destinata a mostrare contenuto HTML come le applicazioni Shiny.
Una tipica sessione di lavoro in R con Rstudio prevedere un utizzo semi-simultaneo di questi pannelli, e principalmente dello Script e del Terminale o Console. Dopo queste premesse siamo pronti per rompere gli indugi e fare conoscenza con R. Qualsiasi sia la vostra installazione, aprite il terminale e cominciamo.
4.4 Le Espressioni
R è, prima di tutto, un ambiente per calcolo. In questo senso, possiamo vedere il terminale come una calcolatrice. E’ possibile eseguire calcoli semplici o complessi direttamente mediante il terminale, digitando delle istruzioni analoghe alle formule algebriche, cioè utilizzando un insieme di quantità numeriche, simboli e operatori matematici, e poi premendo il tasto INVIO. Come avviene per altri ambienti e linguaggi di programmazione, gli operatori matematici di base sono:
- La somma, codificata col simbolo +.
## [1] 7- La sottrazione, codificata col simbolo -.
## [1] -3- La moltiplicazione, codificata col simbolo *.
## [1] 10- La divisione, codificata col simbolo /.
## [1] 0.4- L’elevamento a potenza, codicato col simbolo ^ (ad esempio x^2 indica x elevato al quadrato).
## [1] 32Esistono poi altre simbologie con un significato matematico definito, come ad esempio:
- Il simbolo : che serve a generare una sequenza ordinata di interi tra un minino ed un massimo definiti, come ad esempio
## [1] 1 2 3 4 5 6 7 8 9 10- Il simbolo % che serve, ad esempio, per specificare il prodotto scalare invece che quello generico (vettoriale se utilizzato su vettori), come ad esempio
## [,1]
## [1,] 85All’interno di R, l’utilizzo delle varie tipologie di parentesi è legato a funzionalità diverse (vedi più avanti). Per questo motivo, le parentesi ** tonde ** sono, di fatto, l’unica tipologia di parentesi che mantiene (anche) un significato matematico. Ad esempio
## [1] 10Questo implica che, se esistono espressioni annidate, dovremo utilizzare sempre e solo le parentesi tonde (invece che passare alle quadre e poi alle graffe come ci hanno insegnato a scuola):
## [1] 7.5E’ ovvio che l’utilzzo delle parentesi deve essere sempre “simmetrico” (una parentesi apre e una chiude) e coerente (i conti devono tornare e quindi ci devono essere tante parentesi aperte quanto quelle chiuse). Quando le espressioni diventano molto complesse, quindi, diventa complicato capire, a colpo d’occhio, quali sono le coppie di parentesi. Ad esempio:
## [1] 243Comunque i più comuni editor per gli script, e quindi anche software più complessi e integrati come R studio, ci vengono in soccorso evidenziando le coppie di parentesi quando ci spostiamo lungo una espressione con le frecce destra e sinistra della tastiera (provare per credere!). Le frecce in alto e in basso, invece, possono essere usate per scorrere nella cronologia dei comandi che abbiamo inserito tramite il terminale. Questo ci aiuta a non dover ri-digitare daccapo un’istruzione usata poco prima. Possiamo digitare le espressioni, dunque, attraverso il terminale che, abbiamo già imparato, ci appare come il simbolo >. Tuttavia, quando digitiamo un’espressione matematicamente incompleta (nella quale, ad esempio, manca una parentesi o un argomento legato ad un operatore), R non eseguirà il calcolo ma ci risponderà con l’operatore + che serve a farci capire che “manca qualcosa”. E’ possibile (ma è preferibile non farlo per non pasticciare il codice) inserire più espressioni, separate da ; o . nella stessa linea di comando (prima di premere INVIO). In ogni caso, le espressioni digitate direttamente nel terminale non vengono salvate in memoria e non possono essere usate per produrre risultati molto complessi. Tutte le volte che sono necessari più passaggi per arrivare dai dati di partenza ai risultati finali è necessario “prendere appunti”, cioè generare delle quantità intermedie e associare ad esse dei nomi. Questo è esattamente quello in cui consiste l’ assegnazione.
4.5 Le Assegnazioni
Il risultato di una semplice espressione, come gli esempi del paragrafo precedente, viene stampato sullo schermo, cioè appare come risposta di R nel terminale, ma non viene memorizzato. Per generare una costante, una variabile o un qualsiasi oggetto che contenga uno o più valori (che magari solo il risultato di espressioni matematiche) è necessario assegnare all’espressione un nome. Questo è possibile farlo attraverso i comandi = e <-. Ad esempio:
hanno lo stesso significato e producono il medesimo effetto: l’oggetto a sarà associato alla quantità 4. Perché questa ridondanza (2 simbologie per la stessa cosa)? In realtà, = e <- non si comportano esattamente allo stesso modo. Per cogliere la differenza, proviamo a digitare la seguente espressione, basata sull’utilizzo della funzione sum:
## [1] 9## [1] 4Dopo che R ci avrà restituito il risultato 9, proviamo a “chiedergli” se ricorda quanto valgono a e b, ad esempio digitando a nel terminale e premendo invio. Scopriremo che R non ricorda quanto valga a! Se invece provassimo a digitare l’espressione:
## [1] 9## [1] 4e poi chiedessimo a R quanto vale a (oppure b) scopriremmo che R ha memorizzato i loro valori. Il perchè di questa apparente stranezza sta nel fatto che l’ambiente di calcolo di R non è unico, bensì ogni funzione opera in un suo “spazio” secondario e solo le quantità assegnate con <- trascendono dal sottospazio definito dalla funzione sum allo spazio generale attraverso il quale dialoghiamo. Dunque, a seconda che vogliamo assegnare delle quantità “generali” o “locali” sceglieremo la simbologia corrispondente, tenendo presente che esistono delle “buona pratiche” che vedremo più avanti. Ovviamente una differenza sostanziale tra = e <- sta anche nella complessità (e quindi nella velocità) delle due scritture: nel secondo caso, dovremo usare una combinazione due tasti (< + -) invece che uno, e quindi l’assegnazione “generale” è più “faticosa”. Un’ultima precisazione: le assegnazioni possono essere scritte anche da sinistra verso destra. Ad esempio le scritture:
sono funzionalmente equivalenti. Tuttavia si sconsiglia la seconda poichè, come chiunque può sperimentare, è molto più chiaro un algoritmo in cui gli oggetti generati nei diversi passaggi compaiono subito all’inizio di ogni riga.
4.6 Sintassi di base (I): l’uso delle parentesi
Le parentesi sono dei simboli tipografici ampiamente usate sia nella lingua scritta che nella matematica. Esistono 3 tipi di parentesi, e per ognuno di essi esiste una versione di apertura delle parentesi ed una di chiusura: la prima è generalmente un’immagine dotata di convessità verso sinistra, mentre la seconda la possiede generalmente a destra. Nell’ambiente R, le parentesi sono delle strutture molto importanti usate per finalità ben precise. Per questo è fondamentale imparare ad usarle in modo appropriato ed imparare a riconoscerele all’interno di uno script, in modo da orientarsi in procedure complicate o istruzioni annidate. All’interno di R, ognuna delle tre diverse tipologie di parentesi (tonde, quadre, graffe) è destinata a uno scopo preciso:
4.6.1 Le parentesi tonde
Servono per specificare gli argomenti (ed eventualmente le opzioni) di una funzione. In sostanza, le parentesi tonde deliminato un micro-ambiente, parzialmente indipendente da quello generale, all’interno del quale entrano alcuni oggetti o valori (gli argomenti) e dal quale fuoriescono altri oggetti o valori (i risultati). Può essere utile, a questo punto, fare un piccolo antipasto di come si usano le funzioni in R (torneremo estesamente più avanti sull’argomento). L’esempio seguente ci mostra il risultato dell’utilizzo della funzione c, una delle più semplici tra quelle di base.
## [1] 1 2 3 5Il nome c sta per concatenate (concatena), e difatti questa funzione mette insieme gli argomenti, separati da virgole, in un singolo oggetto (in questo caso un vettore composto da 4 numeri). Le parentesi tonde seguono sempre il nome della funzione e racchiudono gli argomenti (e le opzioni, se ci sono) separati da virgole. In questo caso non abbiamo effettuato nessuna assegnazione, e il terminale di R esegue il comando restituendoci il vettore desiderato. Un altro semplice esempio è:
## [1] 11In questo caso, abbiamo generato un vettore denominato a e poi abbiamo applicato la funzione sum (somma) su di esso, ottenendo il risultato corrispondente alla somma degli elementi di a. Gli argomenti di una funzione, dunque, sono i dati in ingresso, la materia prima per permettere alla funzione di lavorare e restituirci un risultato.
4.6.2 Le parentesi quadre
Servono per indicizzare gli oggetti, cioè per identificare al loro interno delle sottoparti precise. Come all’interno di una griglia spaziale (immaginate di giocare una partita di battaglia navale), le parentesi quadre ci permettono di fare riferimento a pezzi specifici di oggetti complessi, permettendoci di manipolarli (estrarne delle parti, sostituirle, modificarle, ecc.). Anche in questo caso si possono fare degli esempi preliminari.
## [1] 10La scrittura precedente definisce un nuovo vettore a e poi, mediante l’uso delle parentesi quadre, ne identifica e isola il primo valore (in questo caso il numero 10). Naturalmente potremmo isolare, con la stessa logica, un altro elemento di a, per esempio il quarto.
## [1] 5Dovrebbe essere chiaro, quindi, che il numero che compare tra le parentesi quadre corrisponde alla posizione dell’elemento desiderato, e non al suo valore. Siccome un vettore di numeri è, per definizione, un oggetto unidimensionale, è sufficiente un singolo valore (la “posizione nella fila”) per indicare un singolo valore (come nella coda alle poste). Ma cosa accade quando abbiamo oggetti con più di una dimensione? Per comprenderlo estendiamo gli esempi alle matrici (che sono oggetti a due dimensioni, righe e colonne). Vediamo un esempio:
## [,1] [,2] [,3]
## [1,] 101 104 107
## [2,] 102 105 108
## [3,] 103 106 109## [1] 101Sorvoliamo sull’analisi degli argomenti della funzione matrix (i lettori più scaltri avranno intuito che la funzione la genera mettendo i valori da 101 a 109 in 3 righe e 3 colonne, come si vede dalla struttura che R stampa sullo schermo quando invochiamo m), e vediamo come, in questo caso, all’interno delle parentesi quadre abbiamo messo 2 numeri, 1 e 1, separati da una virgola. R ci dice che m[1,1] corrisponde al numero 101, quello collocato nella prima riga e prima colonna della matrice. Allo stesso modo potremmo identificare il numero 104 come quello nella prima riga e seconda colonna.
## [,1] [,2] [,3]
## [1,] 101 104 107
## [2,] 102 105 108
## [3,] 103 106 109## [1] 104Insomma i due valori separati da virgola tra le quadre sono niente altro che le coordinate dei valori desiderati. Nel caso di un oggetto bidimensionale come una matrice, per indicare un elemento si deve ragionare come in una partita di battaglia navale!
Naturalmente possiamo voler isolare più di un elemento di un oggetto complesso, ad esempio:
## [,1] [,2] [,3]
## [1,] 101 104 107
## [2,] 102 105 108
## [3,] 103 106 109## [,1] [,2]
## [1,] 101 104
## [2,] 102 105In questo caso, abbiamo isolato un pezzo della matrice m, corrispondente alle prime 4 celle (quelle nelle prime due righe e prime due colonne) e lo abbiamo assegnato all’oggetto n. Un ultimo esempio, la selezione di elementi non contingui:
## [,1] [,2] [,3]
## [1,] 101 104 107
## [2,] 102 105 108
## [3,] 103 106 109## [,1] [,2]
## [1,] 101 107
## [2,] 103 109Analizzando il codice dell’esempio, dovremmo poter capire che, all’interno delle quadre, abbiamo indicato due vettori generati con la funzione c. Ciascuno di essi corrisponde al vettore composto da due elementi, i numeri 1 e 3, e quindi il risultato complessivo sarà la creazione di un oggetto n, anch’esso una matrice, composto dagli elementi nella prima riga e terza colonna di m. Torneremo sul concetto di indicizzazione, e sul suo utilizzo, man mano che prenderemo familiarietà con oggetti aventi struttura più complessa (come ad esempio le liste o gli array)
4.6.3 Le parentesi graffe
Servono principalmente a delimitare strutture precise come i loop (cicli). Dunque le vedremo comparire all’interno di un codice per generare e gestire delle strutture di controllo complesse come le scelte (il ciclo if, else) o iterazioni di blocchi di istruzioni (il ciclo for). Un esempio è:
## [1] 10In questo caso, abbiamo definito tre oggetti ( a, b, e c), e poi abbiamo usato la struttura di controllo for per iterare una semplice operazione: prendere a e sommargli b volte c. Il risultato, intuitivo, è 10. Le graffe servono per racchiudere il ciclo for. E’ interessante notare che, manipolando i valori di a, b e c, si possono ottenere risultati diversi… il che è esattamente lo spirito di una struttura iterativa del genere. Vedremo che le parentesi graffe servono anche a definire le funzioni, ma su questo torneremo più avanti.
4.7 Tipologie di dati: gli attributi e le classi
Tutti i linguaggi di programmazione a oggetti (ed R è uno di questi) sono basati sul fatto che blocchi di informazione detti oggetti (siano essi quantità, variabili, istruzioni, procedure complesse) siano utilizzati per accedere ad altrettanti blocchi di dati in memoria. Questa è una differenza sostaziale rispetto ad altri linguaggi come C che si basano sull’accesso diretto ai dati in memoria, cosa che R non consente. All’interno di R gli oggetti hanno un nome esclusivo e sono l’elemento di base su cui lavorare, qualsiasi sia la loro struttura. Il modo in cui R immagazzina in memoria una dato oggetto è detta tipo dell’oggetto stesso. Non è importante approfondire i diversi tipi di oggetti in R, per cui non ci dilungheremo sull’argomento.
Quello che, invece, è veramente importante sapere è che ogni tipo di oggetto possiede una serie di attributi. Tra questi, quello che spicca per importante è la Classe. Come abbiamo già detto in precedenza, le classi sono importanti poichè a seconda di essere variano i metodi che si possono applicare agli oggetti. A questo punto è utile chiarire che i metodi non sono altro che funzioni, e che quindi a ogni classe di oggetti possono essere applicate funzioni diverse, ovvero che una stessa funzione può avere comportamenti diversi a seconda della classe dei suoi argomenti (cioè degli oggetti sui quali viene applicata).
All’interno di R è possibile operare con diverse tipologie di dati, per ognuna della quali esiste una classe predefinita. Sebbene ci siano molte classi già implementate ed altre possano essere definite dagli utenti esperti, esistono 5 classi principali di dati:
- La classe numeric, destinata a tutti i numeri reali (elementi dell’insieme R)
- La classe integer, destinata a tutti i numeri interi (elementi dell’insieme N)
- La classe character, destinata alle stringhe di testo o alle sequenze di caratteri
- La classe logical, destinata alle espressioni nell’accezione dell’Algebra di Boole
- La classe factor, destinata a variabili o quantità qualitative o semi-quantitative
E’ facile immaginare il senso delle prime due classi, poichè si riferiscono a insiemi ben noti della matematica. Anche la terza classe è intuitivamente familiare: tutti sappiamo cosa sono i caratteri di un testo. Per gli altri è sufficiente dire che il testo (formato da caratteri) è un tipo di informazione particolare per gli ambienti di calcolo (come R), poichè se ne possono valutare le caratteristiche (quanti caratteri ci sono in una stringa? Quante parole ci sono in un testo?) ma non ha senso applicare funzioni matematiche ai testi. La quarta classe si riferisce agli oggetti (le espressioni, ma in un senso diverso da quello di cui abbiamo parlato in una sezione precedente a proposito di R) propri dell’Algebra di Boole, il grande matematico inglese che ha gettato le basi per la computazione elettorica. L’ultima classe è pensata per permetterci di gestire valori semi-quantitativi o qualitativi. Si possono fare moltissimi esempi di “fattori” (variabili che possono assumere un numero finito di stati o valori): il sesso di ciascun individuo di una popolazione, il colore degli occhi di diversi individui, la classe di età (coorte) a cui appartengono, l’intensità di un trattamento farmacologico. La cosa importante da dire, in proposito, è che possono esserci fattori ordinabili e fattori non ordinabili. Un esempio del primo tipo sono il sesso o il colore degli occhi: non ha senso dire che maschio viene prima di femmina o che ci sia una scala ordinata di colori (o forse si?). Esempi di fattori ordinabili sono invece la classe di età (coorte) o l’intensità di un trattamento farmacologico: è possibile stabilire una sequenza continua di valori (es. classe di età 0, classe 1, classe 2 e così via).
Per ciascuna delle 5 classi esiste un comando (funzione) che serve a generare un oggetto appartenente alla classe voluta. I comandi in questione hanno lo stesso nome della classe, e quindi avremo le funzioni:
- numeric()
- integer()
- character()
- logical()
- factor()
L’utilizzo di queste funzioni è abbastanza intuitivo. Ad esempio, la funzione numeric può essere utulizzata con un solo argomento ( length, ovvero lunghezza) per generare un vettore numerico pieno di zeri (0 è il valore di default) di dimensione desiderata.
## [1] 0 0 0 0 0Lo stesso avviene per integer, character, e logical
## [1] 0 0 0 0 0Nel caso di integer non c’è molto da dire.
## [1] "" "" "" "" ""Nel caso di character otteniamo una sequenza di blocchi di testo vuoti.
## [1] FALSE FALSE FALSE FALSE FALSENel caso di logical otteniamo una sequenza di espressioni booleane, per definizione false (che è il corrispettivo di 0 nell’Algebra binaria di Boole, mentre 1 corrisponde a true). Una piccola trattazione dell’Algebra di Boole, così importante per la programmazione, ci aspetta più avanti.
Una cosa che merita di essere detta, inoltre, è che R è in grado di riconoscere automaticamente le caratteristiche di un oggetto e assegnarlo alla classe opportuna. Proviamo a riprendere uno degli esempi precedenti e, dopo aver generato una variabile di nome a alla quale assegnamo valore 4, usiamo la funzione class() per chiedere a R che roba sia a.
## [1] "numeric"In questo esempio, R ha correttamente dedotto che volessimo generare una quantità numerica. In effetti, avremmo potuto anche scegliere di assegnare a alla classe integer. Tuttavia R sceglierà sempre come default la classe numeric (che è un sinonimo di double per chi ha già familiarità con linguaggi di programmazione, e in effetti double è il tipo degli oggetti numeric, cioè il modo con cui viene archiviato in memoria) per tutti gli oggetti che contengono solo numeri.
E’ anche possibule definire un oggetto senza inserirne direttamente il valore, e l’esempio che segue ci permette anche di riprendere il concetto di eredità (inheritance).
## [1] 7## [1] "numeric"In questo esempio abbiamo definito la quantità a come la somma della radice quadrata di 9 (la funzione sqrt è appunto l’acronimo di square root) e del numero 2 elevato al quadrato. Interrogato sul valore di a e sulla sua classe, R ci risponde che a vale 7 e che è un numeric. R ha automaticamente calcolato il risultato e lo ha assegnato all’oggetto a. Inoltre, ha dedotto che a è un oggetto della classe numeric, e questo è precisamente un esempio di eredità della classe.
4.8 Strutture di dati
A questo punto, dopo aver visto quali sono le principali tipologie di dati che si possono gestire in R, dobbiamo comprendere in quali modi è possibile organizzarli. L’oggetto più semplice all’interno di R è il vettore, ma strutture di base sono anche le matrici, gli array, le liste e, infine, i data frame (che possono essere considerati degli oggetti “speciali”).
4.8.1 Vettori
Un vettore può essere pensato come una serie di celle concatenate, ognuna delle quali contiene un valore. A ciascuna cella o elemento del vettore corrisponde un indice di posizione che, come nel caso dei numeri civici su una via che consentono a un corriere postale di trovare un destinatario specifico, possono essere usati per manipolare il vettore, ad esempio estraendone i valori presenti in celle precise identificate tra quadre in una indicizzazione. La cosa importante da assimilare è che un vettore può contenere elementi che appartengono tutti a una stessa classe. Questo vuol dire che R gestisce vettori di tanti tipi, i principali dei quali sono proprio i character, integer, logical, numeric…. insomma proprio le classi che abbiamo visto poco fa. Esistono anche altri tipi di vettori, che menzioniamo senza approfondire: complex (numeri complessi), double, expression, list, single, e raw. Generare un vettore è molto semplice, e non indicheremo due modalità alternative:
- Mediante la sua “funzione generatrice”. Ne esiste una per ogni tipo di vettore, e il suo nome è intuitivo. Ad esempio, per generare un vettore numeric c’è la funzione omonima numeric. Il suo utilizzo, come quello delle sue “sorelle” character, logical, integer, e factor (ma vale anche per gli altri tipi appena menzionati), è molto semplice:
## [1] 0 0 0 0 0 0 0 0 0 0## [1] "numeric"L’argomento all’interno delle parentesi specifica la lunghezza del vettore che si vuole generare. Si noterà che, per default, R ha generato un vettore composto da 10 quantità tutte uguali a 0. Intuitivamwente, la funzione character genera una serie di stringhe di lunghezza 0 (vuote).
## [1] "" "" "" "" "" "" "" "" "" ""## [1] "character"Se non lo avete già notato, le quantità character sono sempre facilmente identificabili perchè R le racchiude tra le virgolette. In entrambi gli esempi, l’applicazione della funzione class sugli oggetti generati restituisce una risposta analoga a quelle viste nel paragrafo precedente, e naturalmente univoca perchè tutti gli elementi del vettore sono della stessa classe.
- Mediante la funzione c, che abbiamo già incontrato:
## [1] 1 2 3## [1] "numeric"## [1] "A" "B" "C"## [1] "character"Noterete che nel primo caso abbiamo messo insieme (concatenato) 3 numeri per generale il vettore a, immediatamante classificato da R come numeric. Nel secondo caso abbiamo messo insieme le prime tre lettere dell’alfabeto, ottenendo un vettore che R classifica come character.
Per ciascuna delle funzioni generatrici esiste una sorella “coercitrice”. Per esempio a numeric corrisponde is.numeric, così come a character corrisponde is.character. Vediamo un esempio illuminante.
## [1] 1 2 3## [1] "numeric"## [1] "1" "2" "3"## [1] "character"In questo caso abbiamo prima generato un vettore numeric e poi lo abbiamo “costretto” a diventare character. A volte i neofiti di R sono confusi da alcuni aspetti di queste trasformazioni, per cui vediamo cosa succede caso per caso.
## [1] "1" "2" "3"## [1] 1 2 3## Warning: si è prodotto un NA per coercizione## [1] NA NA NANei primi due casi è andato tutto bene. Infatti, quando R ha coercito il vettore “1”, “2”, “3” a diventare numeric ha ottenuto dei numeri… cioè delle quantità che per lui hanno senso e possono essere gestite come tali. Ma, quando abbiamo coercito il vettore “A”, “B”, “C” a diventare numeric, R non ha ottenuto dei valori gestibili come numeric e ha quindi generato dei valori detti NA (not assigned). Questa è la prima volta che ci imbattiamo in loro, e dobbiamo subito sapere che la loro comparsa può essere un indice cdel fatto he qualcosa nei nostri calcoli è andato storto. Magari c’è un “errore” da qualche parte nel nostro codice. Invece:
## [1] A C C
## Levels: A C## [1] 1 2 3
## Levels: 1 2 3## [1] A C C
## Levels: A B C## [1] "A" "C" "C"## [1] 1 3 3Guardiamo per bene questi esempi, anche perchè ne approfitteremo per illustrare la funzione generatrice factor. Nel primo esempio, abbiamo definito il vettore a concatenando tre valori, due dei quali sono uguali tra loro, in modo da generare un vettore character che poi abbiamo coercito a diventare factor. Poichè gli univoci nel vettore di partenza erano solo due (“A” e “C”), R ha automaticamente stabilito che il factor a contiene valori che possono assumere solo uno tra questi due possibili stati. Gli stati o valori che possono essere assunti da un factor si chiamano livelli. I livelli possono essere esplicitamente definiti mediante la funzione generatrice factor o possono essere “desunti” dall’analisi dei valori assunti dagli elementi di un oggetto già esistente, come avviene anche nel secondo esempio (in cui abbiamo generato un numeric e poi lo abbiamo trasformato in un factor). Il terzo esempio, invece, ci mostra come possiamo generare un vettore factor definendo i suoi livelli in modo che comprendano stati o valori che non sono osservati nel vettore stesso, ma sono teoricamente ammessi. Nello specifico, a comprende solo tre elementi che assumono uno tra due valori (“A” e “C”), ma il livello “B” è ammesso anche se non osservato.
Sorvoleremo sulle altre combinazioni di coercizione, ma il neofita è invitato a sperimentare e apprendere in maniera euristica…
Invece è importante richiamare l’attenzione su un aspetto già menzionato di R: la sua logica ad oggetti è concepita per essere vettoriale. Questo significa che vettori e matrici sono le sue strutture di base, e di fatto ogni oggetto può essere visto come un qualche tipo di vettore. Addirittura gli scalari possono essere visti come speciali vettori di dimensione 1 (un unico elemento). Le conseguenze di questa cosa sarà evidente nel prossimo paragrafo.
4.8.2 Matrici (e Array)
Ed eccoci qui a parlare di matrici. La prima cosa da dire a proposito di esse è che sono uno degli oggetti elettivi per il calcolo all’interno di R. Moltissime funzione di base, infatti, sono già predisposte per essere applicate sulle matrici in diretta e “performante” in termini di tempo di esecuzione. Ma cosa è una matrice? Una matrice può essere definita come un reticolo (in inglese lattice) di valori omologhi (nel senso che appartengono tutti alla stessa tipologia, per esempio sono tutti numeric o tutti character) disposti in maniera regolare in righe e colonne. Ogni valore sarà pertanto individuato in maniera univoca da una coppia di numeri interi che corrisponde ai suoi indici di posizione all’interno della matrice (riga e colonna). Questa logica topografica è la stessa che utilizzavamo quando giocavamo alla battaglia navale sui banchi di scuola. La sintassi del comando che si deve usare per generare una matrice è molto semplice. Quello che occorre è specificare il contenuto della matrice e la sua geometria (quante righe, quante colonne).
#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
M <- matrix(data = 1:6, nrow = 3, ncol = 2)
M## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6Questo primo, banale esempio ci aiuta a capire 2 cose importanti:
Quando visualizziamo una matriche, R utilizza l’indicizzazione per mostrarci la sua struttura reticolare. Infatti all’inizio di ogni riga e sopra ogni colonna compaiono due parentesi quadre con all’interno i rispettivi indici di riga e di colonna.
Nel comando predente abbiamo speficato che l’argomento data (cioè il contenuto della matrice) deve corrispondere ai numeri da 1 a 6. Ebbene, R dispone questi numeri in 2 colonne e partendo dall’angolo sinistro e procedendo a riempire la matrice “per colonne”.
In effetti, il comando matrix ha un’opzione che ci permette, se lo vogliamo, di riempire la matrice “per riga”:
#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
M <- matrix(data = 1:6, nrow = 3, ncol = 2, byrow = T)
M## [,1] [,2]
## [1,] 1 2
## [2,] 3 4
## [3,] 5 6In questo esempio, l’attivazione dell’opzione byrow ci ha restituito un oggetto con lo stesso contenuto della matrice precedente ma con una diversa disposizione dei numeri al suo interno. In entrambi i casi, comunque, la matrice può essere vista come una serie di vettori (righe o colonne) appiccicati insieme. Una dimostrazione di questo ci viene dall’utilizzo dei comandi cbind e rbind (acronimi di “columns bind” e “rows bind”):
#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
c1 = 1:3
c2 = 4:6
M <- cbind(c1, c2)
M## c1 c2
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6## [1] "matrix" "array"## [,1] [,2] [,3]
## c1 1 2 3
## c2 4 5 6## [1] "matrix" "array"In entrambi i casi otteniamo un oggetto di classe matrix. Da questi semplici esempi si deduce che una matrice è un oggetto sempre e solo bidimensionale. Ebbene, per comprendere gli array basta sapere che essi sono semplicemente matrici sono più di 2 dimensioni. Non ci dilunghiamo oltre sulle matrici, ma torneremo estesamente su di esse quando (tra poco) parleremo di funzioni.
4.8.3 Liste
Le liste sono delle vere e proprie “collezioni” di oggetti in R. Ogni lista è di per se un oggetto, ma in pratica ogni lista contiene dei sotto-oggetti (matrici, vettori, scalari, array, data frame, altre liste).
L’utilità delle lista sta proprio nella loro versatilità strutturale: mentre vettori, matrici ed array sono oggetti che contengono elementi di un solo tipo, le liste possono contenere una molteplicità di sotto-oggetti di tipo diverso. Inoltre, tutti gli altri oggetti di R sono “regolari”: la loro struttura è organizzata in dimensioni (le righe o le colonne) rigide: ci si aspetta che ogni riga di una matrice contenga un elemento per ciascuna colonna, e viceversa.
Per comprendere la differenza tra le liste e gli altri oggetti, può essere utile fare un giro all’Ikea.
La figura parla da se: non potreste mai mettere la TV in una matrice o in un vettore!
E’ possibile generare una lista mediante il comando list di cui vediamo una prima semplicissima applicazione:
## [1] 4 9 1 0 7#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
M <- matrix(data = 1:6, nrow = 3, ncol = 2)
M## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6## [[1]]
## [1] 4 9 1 0 7
##
## [[2]]
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6Si vede subito che all’interno di L ci sono sia V che M. Ora, prima di passare alle funzioni (che abbiamo subdolamente introdotto senza parlarne in maniera esplicita…), vediamo l’ultima tipologia di oggetto R di base: i data.frame
4.8.4 Data Frame
E’ abbastanza facile immaginare un data frame come una matrice, quindi un oggetto regolare, che contenga diversi tipi di oggetti, tipicamente un tipo per ogno colonna. Ad esempio
#Genero il vettore V avente 5 elementi numerici
V <- c(4, 9, 1, 0, 7)
#Genero il vettore C avente 5 elementi character
C <- c("A","A","B","B","C")
#Genero il vettore H avente 5 elementi factor
H <- factor(c("L1","L2","L2","L2","L1"), levels = c("L1", "L2"))
#Genero il data frame df contente gli oggetti V, C e H
df <- data.frame(V, C, H)
df## V C H
## 1 4 A L1
## 2 9 A L2
## 3 1 B L2
## 4 0 B L2
## 5 7 C L1Comodo no? Immaginate di essere un ecologo intento nel monitoraggio di una popolazione animale “sul campo”. Per ogni indivduo analizzato (la riga del data frame) raccoglierete una serie di misure. Alcune continue (il peso, la lunghezza), altre character (il nome o il codice dell’esemplare), altre factor (il sesso), e così via. Vi sarà possibile organizzare queste molteplici informazioni nelle colonne di un data frame in modo da avere il corrispondente informatico di una tabella. E’ chiaro che tutto questo è molto intuitivo e versatile, e questo è esattamente il motivo per cui, nella maggior parte dei corsi su R, i data frame sono un argomento centrale e questi oggetti sono considerati i più importanti all’interno di R.
Tuttavia, da un punto di vista computazionale, i data.frame sono oggetti da prendere con pinze. Questo anche perchè per usare i data frame è necessario avere una certa famigliarità con tutte le tipologie di dati (numeric, character, factor, ecc.) Torneremo in maniera apporondita sui data frame quando affronteremo le diverse “filosofie” per produrrre grafici, ma per ora li mettiamo da parte.
4.9 Sintassi di base (II): le funzioni
Abbiamo già spiegato che R è un ambiente object-oriented e, quindi, la manipolazione e trasformazione dei dati contenuti negli oggetti rappresenta in estrema sintesi il metodo di lavoro che si utilizza in questo ambiente. Le funzioni non sono altro che sequenze di istruzioni per manipolare dati in ingresso ed ottenere un certo risultato in uscita. R, anche nella sua versione base, contiene centinaia di funzioni preimpostate e disponibili, ma diciamo da subito che l’utente, anche se è un principiante, può definirne di nuove e, anzi, il successo di R si deve sopratutto alla sua capacità di stimolare la fantasia e la creatività. Per impadronirci di questo strumento essenziale, tuttavia, dobbiamo comprenderne ed assimilarne gli aspetti di base:
- Ogni funzione ha un suo nome preciso, non ambiguo e unico. In generale, non possiamo definire oggetti che hanno lo stesso nome delle funzioni e viceversa (o meglio possiamo farlo, ma a nostro rischio e pericolo);
- Ogni funzione si utilizza mediante il suo nome seguito da una coppia di parentesi tonde al cui interno sono inseriti i riferimenti agli argomenti della funzione e alle sue opzioni;
- argomenti e opzioni sono specifici di ogni funzione. Questo significa che, col tempo, è necessario (e automatico) imparare a memoria tanti nomi di funzioni e dei loro argomenti…
Vediamo alcuni esempi cominciando da una funzione che abbiamo già incontato: la funzione matrix
#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
M <- matrix(data = 1:6, nrow = 3, ncol = 2)In questo esempio di applicazione notiamo che:
- Definiamo un oggetto di nome M mediante assegnazione alla funzione matrix. Questo significa che quello che esce dalla parte destra dell’assegnazione diventerà M;
- Usiamo la funzione mediante il suo nome seguito da una serie di input forniti all’interno di una coppia di parentesi tonde;
- Quello che c’è tra le parentesi tonde è una serie di assegnazioni con tanto di nomi e di valori. Questa è la modalità di utilizzo più “verbose” cioè esplicita a prolissa. In realtà, potremmo omettere i nomi degli argomnti purchè li inseriamo nell’ordina in cui la funzione se li aspetta.
Ad esempio:
#Genero la matrice M avente 3 righe, 2 colonne e contenente i numeri da 1 a 6
M <- matrix(data = 1:6, nrow = 3, ncol = 2)
#Utilizzo equivalente
M <- matrix(1:6, 3, 2)Dunque la funzione matrix, per funzionare, ha bisogno di 3 argomenti: data, nrow e ncol. Il significato dei loro nomi dovrebbe essere intuitivo: data corrisponde ai dati da inserire (i valori nelle celle della matrice), nrow specifica il numero di righe della matrice, ncol specifica il numero di colonne. Non tutti gli argomenti di una funziona hanno la stessa importanza. Nel caso di matrix, la geometria della matrice da creare (cioè il suo numero di righe e di colonne) è più importante del contenuto. Ce ne accorgiamo provando a fare:
Ad esempio:
## [,1] [,2]
## [1,] NA NA
## [2,] NA NA
## [3,] NA NAL’oggetto M contiene una serie di valori tutti uguali chiamati NA. Scopriremo tra poco di cosa si tratta, ma intanto notiamo che la geometria è quella desiderata. Allo stesso modo, possiamo generare una matrice contenente valori tutti uguali (ma definiti)
## [,1] [,2]
## [1,] 1 1
## [2,] 1 1
## [3,] 1 1In questo caso R ha popolato la matrice con tanti valori pari a 1. E’ interessante commentare cosa succede quando l’input non è “coerente”. Ad esempio:
Ad esempio:
## Warning in matrix(1:7, 3, 2): data length [7] is not a sub-multiple or multiple
## of the number of rows [3]## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6In questo caso abbiamo indicato a R che la matrice deve contenere i valori da 1 a 7, pur avendo 3 righe e 2 colonne (e quindi 6 celle). R, obbediente, produce un oggetto M identico a precedenti omettendo l’ultimo valore da noi indicato per l’argomento data (il 7), ma ci avvisa che “i conti non tornano” mediante un “warning”. Come dice il suo nome, un warning non è un errore ma un avvertimento, ma è importante fare attenzione perchè magari l’incoerenza degli argomenti è frutto di un banale errore di digitazione. Vediamo un altro esempio:
## Warning in matrix(1:5, 3, 2): data length [5] is not a sub-multiple or multiple
## of the number of rows [3]## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 1Se guardiamo bene il contenuto di M, ci accorgiamo che sono presenti i numeri da 1 a 5, inseriti per colonne, ma nell’ultima cella della matrice (quella in basso a destra) compare una seconda volta il numero 1 (il primo della serie da noi indicata). Il motivo è semplice: abbiamo detto a R di generare una matrice di 6 celle ma gli abbiamo fornito solo 5 valori per riempirla. Risultato: R ha “riutilizzato” il primo valore della serie.
Altra cosa da dire importante sulle funzioni è che, oltre agli argomenti (indispensabili), può essere importante conoscere e padroneggiare le opzioni. Riprendiamo l’esempio di matrix
## [,1] [,2]
## [1,] 1 2
## [2,] 3 4
## [3,] 5 6## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6Che differenza notiamo tra questi due comandi? Nel primo caso R ha usato la sequenza da 1 a 6 per riempire la matrice M “per colonna”, nel secondo caso lo ha fatto “per riga”. Questo ci permette di chiarire in senso generale l’uso delle opzioni: esse rappresentano dei comandi di input delle funzioni per alterarne il comportamento ma, essendo appunto opzionali, esiste una modalità “di base” (o di default come dicono gli inglesi) nell’esecuzione di ogni funzione e le opzioni hanno il potere di alterarla. Per disattivare un’opzione dobbiamo porla uguale a FALSE, se la vogliamo attivare la dobbiamo porre uguale a TRUE. Questa è un’altra peculiarità delle opzioni: sono delle variabili booleane e possono assumere solo due valori, TRUE e FALSE appunto. Se comprendiamo questo, possiamo facilmente intuire perchè le opzioni sono sempre per definizione disattive e siamo noi a doverle “attivare”.
Ad esempio:
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6Questi due comandi producono risultati identici perchè sono identici: nel secondo caso l’opzione byrow è espressamente ed esplicitamente annullata dall’utente, nel primo lo è perchè quello è lo stato predefinito di ogni opzione. Questo punto ci fornisce l’appiglio per introdurre una nuova, semplice funzione: sum. Come dice il suo nome, la funzione sum calcola la somma degli oggetti che le vengono forniti come input, indipendentemente dalla loro geometria (possono essere vettori o matrici o array) ma non dal loro tipo (la somma è definita solo per le quantità integer e numeric, non per quelle factor o character o per le altre). Quindi:
## [1] 21## [1] 21Ok? Allora adesso introduciamo volutamente un esempio “rognoso”:
## [1] 1 3 5 -2 3 7## Warning in sqrt(V): Si è prodotto un NaN## [1] 1.000000 1.732051 2.236068 NaN 1.732051 2.645751## [1] NaNAnalizziamo il pasticcio che abbiamo combinato:
- Abbiamo definito il vettore V come composto da 6 elementi numerici, di cui uno negativo
- Abbiamo usato la semplice funzione sqrt (acronimo di square root) per calcolare le radici quadrate dei valori di V
- Siccome non esiste un numero reale che corrisponda alla radice quadrata di un negativo, il nuovo vettore V contiene un valore “strano” che non abbiamo mai incontrato: NaN (acronimo di not-a-number)
- Siamo andati avanti generando la matrice M come se nulla fosse…
- Quando abbiamo calcolato il valore della somma SM di M, abbiamo ottenuto una brutta risposta: ancora un NaN!!!!
Perchè ci siamo andati a impelagare in questa brutta storia? Per mostrare che la funzione sum ha un’utilissima (ma pericolosa!) opzione denominata na.rm. Proviamo ad attivarla:
## Warning in sqrt(V): Si è prodotto un NaN## [1] 9.345921Questa volta abbiamo ottenuto un valore “buono” della somma di M. Se facciamo due calcoli a mente possiamo facilmente dedurre che esso corrisponde alla somma di tutti i valori di M tranne quello strano e brutto NaN, con il quale faremo conoscenza tra poco. Adesso però ci interessa un’altra cosa: l’opzione na.rm sta per “remove NA or NaN”, e quindi significa autorizzare la funzione a far finta che non ci siano valori strani. Quindi, attivandola, abbiamo detto a R di calcolare la somma solo sugli altri valori. A questo punto qualcuno di voi lettori si starà chiedendo: e perchè mai questa fantastica opzione è disattiva di default e dobbiamo attivarla noi? Non sarebbe meglio se fosse sempre accesa e ci proteggesse da risultati brutti? La risposta è NO, non sarebbe affatto meglio, perchè il fatto che i nostri calcoli si inceppino ogni volta che da qualche parte compare un valore strano è un ottimo modo per costringerci a ricontrollare le nostre procedure e fare in modo che siano il più generali e versatili possibili. Per esempio, vogliamo risolvere un problema ma non prendiamo in considerazione che i valori di alcune variabili possono assumere valori negativi. Se così è, e da qualche parte nel nostro codice usiamo funzioni non definite sull’insieme R dei numeri reali (come la radice quadrata o il logaritmo) ci imbatteremo in un valore anomalo e saremmo naturalmente portati a rimediare.
Ci soffermiamo ora su un altro aspetto essenziale delle funzioni. Mi riferisco al fatto che ciascuna di esse vive e opera in un sottoambiente di quello principale, cioè la sessione di lavoro all’interno della quale stiamo operando. Vediamo cosa significa con un esempio:
## [1] 5## [1] 5## [1] 3Sebbene avessimo definito x e y con valori pari a 5 e 3, la somma (in cui abbiamo ri-definito i valori di x e di y), ci ha restituito come somma 0. Inoltre, nell’ambiente principale i valori di x e di y sono rimasti quelli “originali”. Questa ultima cosa dipende dal fatto che, all’interno della funzione sum, abbiamo usato l’uguale (=) invece dell’assegnazione (<-). Infatti, se facciamo il contrario:
## [1] 5## [1] 5## [1] 0scopriamo che ora il valore di y è cambiato anche nell’ambiente principale. Questo è il motivo per cui, nell’ambito delle “buona pratiche” che affronteremo più avanti, è sempre proibito fare assegnazioni nello sviluppo di codici e pacchetti: si rischia di fare un pasticcio tremendo quando le si utilizza perchè si rischia di sovrascrivere quantità e oggetti dell’ambiente principale.
4.10 Il mondo “a matrioske”
Il mondo delle funzioni di R è fatto come le famose bambole russe, nel senso che ogni funzione generalmente può accettare, al posto dei sui argomenti, delle altre funzioni, a patto che restituiscano oggetti coerenti con gli input attesi dalla funzione di Rango superiore.
Se, ad esempio, volessi generare una matrice che contiene come elementi i valori restituiti dalla funzione somma, scriverò:
In questo caso, la matrice m è rimpita con il solo valore 9, cioè l’output della funzione sum applicata al vettore x. Come avevamo già detto, quello che avviene dentro le funzioni di rango più basso non si riflette (se non tramite i risultati) sulle funzioni di rango più elevato. Ancora un esempio:
## [1] 405In questo semplice esercizio abbiamo “annidato” tre funzioni una dentro l’altra, ottenento il valore finale di s. Il grande vantaggio di questa potenzialità di R è che ci consente di risparmiare sugli oggetti (e i relativi nomi) che è necessario generare. Il prezzo è che, con strutture molto complesse a annidate, può essere difficile modificare il codice o correggerlo.
4.11 La frontiera del calcolo: NA e NaN
Abbiamo recentemente fatto la sgradevole conoscenza del NaN. Questa quantità, “not-a-number”, viene fuori quanto facciamo calcoli che non sono definiti nell’insieme dei numeri Reali. Quindi:
## [1] -Inf## Warning in sqrt(x): Si è prodotto un NaN## [1] NaNOra completiamo l’opera con la conoscenza dei NA, che sono ancora più antipatici. NA sta per “not_assigned”, cioè quantità non definita. Ecco alcuni esempi di come può saltare fuori:
## Warning: si è prodotto un NA per coercizione## [1] NAIn questo caso abbiamo generato un NA chiedendo a R di coercire come numerico una quantità testo, il che letteralmente non ha alcun senso. Più in generale, i NA sono il classico caso di “dato mancante”. Se si trovano all’interno di un oggetto, i NA devono essere interpretati e trattati come dei “buchi”, a differenza dei NaN che sono “valori impossibili”. La presenza dei NA in un codice sono generalmente un sintomo del fatto che la procedura non è abbastanza generale (poichè la presenza di buchi vuol dire spesso che ci sono condizioni che non si realizzano mai, per esempio selezioni che restituiscono un insieme vuoto) e che quindi non è adatta ai dati. Come abbiamo visto, R non nasconde la polvere sotto il tappeto (a meno che non lo invitiamo a farlo), per cui la graduale eliminazione dei passaggi che generano dei NA o dei NaN rappresenta una normale fase di revisione e debugging del codice.
4.12 Operatori relazionali e algebra di Boole
Sull’opera immortale di George Boole è stato scritto tanto, ma mai a sufficienza. Nessuno più di lui ha contribuito a gettare le basi della computazione elettonica. Tanto è vero che la sua Algebra è fondamentale anche (e ancora) per noi. Alla base di tutto c’è che le quantità che maneggiamo sono sempre tradotte, nel profondo dei nostri pc, in quantità binarie. Come nelle sinapsi del nostro cervello, i microchip dei nostri processori riduco la realtà a sequenze di stati acceso-spento.
La prova sta nel fatto che le quantità booleane le abbiamo già incontrate: sono le quantità di tipo logical. Adesso dobbiamo generalizzare a problemi più complessi, per esempio la verifica di condizioni all’interno di funzioni o algoritmi. Per farlo, prima dobbiamo prendere in rassegna la sintassi degli operatori booleani in R:
dB = data.frame(Operatore = c("==", ">", "<", ">=", "<=", "!", "&", "|"),
Significato = c("uguale", "maggiore", "minore", "maggiore o uguale",
"minore o uguale", "negazione","and","or"))
knitr::kable(
dB, caption = 'Gli operatori booleani in R',
booktabs = TRUE
)| Operatore | Significato |
|---|---|
| == | uguale |
| > | maggiore |
| < | minore |
| >= | maggiore o uguale |
| <= | minore o uguale |
| ! | negazione |
| & | and |
| | | or |
Vediamo ora alcune loro semplici applicazioni, in modo da spiegare in maniera intuitiva il loro utilizzo
#Definisco le quantità x e y e faccio a R una serie di domande
x <- 5
y <- 3
x > y #x è maggiore di y## [1] TRUE## [1] FALSE## [1] TRUE## [1] FALSE## [1] TRUEPrestiamo attenzione agli esempi precedenti perchè abbiamo introdotto alcune cose importanti: * Si possono scrivere semplici espressioni proprie dall’Algebra di Boole, ovvero quantità logiche che possono essere solo o vere (TRUE) o false (FALSE) senza ambiguità e complicazioni ulteriori. * In risposta a queste semplici espressioni, R ci restituisce TRUE o FALSE * Se vogliamo usare la negazione o combinare insieme più espressioni dobbiamo racchiuderle tra tonde perchè, di fatto, ogni singola espressione è una piccola funzione
E’ chiaro che tutto questo può esserci utile soltanto se ricordiamo l’Algebra di Boole e, in particolare, le tabelle di verità degli indicatori che si usano per mettere insieme più espressioni.
Questa è la tabella di verità per AND (&):
knitr::kable(data.frame(Espressione1 = c("TRUE","FALSE", "TRUE","FALSE"),
Espressione2 = c("TRUE", "TRUE", "FALSE", "FALSE"),
Valore = c("TRUE","FALSE","FALSE","FALSE")),
caption = "Tabella di verità dell'operatore AND",
booktabs = TRUE
)| Espressione1 | Espressione2 | Valore |
|---|---|---|
| TRUE | TRUE | TRUE |
| FALSE | TRUE | FALSE |
| TRUE | FALSE | FALSE |
| FALSE | FALSE | FALSE |
Questa è la tabella di verità per OR (|):
knitr::kable(data.frame(Espressione1 = c("TRUE","FALSE", "TRUE","FALSE"),
Espressione2 = c("TRUE", "TRUE", "FALSE", "FALSE"),
Valore = c("TRUE","TRUE","TRUE","FALSE")),
caption = "Tabella di verità dell'operatore OR",
booktabs = TRUE
)| Espressione1 | Espressione2 | Valore |
|---|---|---|
| TRUE | TRUE | TRUE |
| FALSE | TRUE | TRUE |
| TRUE | FALSE | TRUE |
| FALSE | FALSE | FALSE |
Per capire l’utilità dell’Algebra di Boole in R possiamo usare alcuni semplici esempi:
## [1] 9 4 6 7 3 3 1## [1] -7 -14## [1] 3 3Dopo aver generato il vettore x, composto di 10 valori numerici, usiamo le parentesi quadre per racchiudere un’espressione che ci permetta di selezione, usando l’algebra di Boole, alcuni degli elementi di x. In questi esempi, estraiamo gli elementi di x che sono positivi, o negativi, o uguali al valore 3. Si tratta ovviamente di esempi molto semplici. Ma la logica da utilizzare per combinazioni più complesse è esattamente la stessa… ma per applicarla dobbiamo fare conoscenza con la funzione which.
La funzione which serve per combinare più condizioni usando gli operatori di Boole. Immaginiamo di voler estrarre da x, in un colpo solo, gli elementi maggiori di 3 o minori di -3.
## [1] 9 4 6 -7 7 -14Naturalmente dobbiamo prestare grande attenzione alla struttura annidata delle parentesi e alla sintassi. Infatti, nel comando precedente, ci sono due condizioni che devono essere valutate, cioè (x > 3) e (x < -3). Poichè esse sono collegate dall’operatore booleano OR (|), è sufficiente che una sola di esse sia soddisfatta. which è, in effetti, una funzione estremamente utile e frequente, che ci permette di assemblare condizioni anche molto complesse.
## [1] 3 3 1In questo esempio abbiamo “rovesciato” la selezione precedente, e quindi abbiamo scelto di estrarre i valori compresi tra -3 e 3 ma con l’esclusione dello zero. Si noti che le due condizioni ((x <= 3)&(x >= -3)) sono racchiuse da una coppia di graffe e quindi il risultato di questa espressione viene prima calcolato e poi combinato con quello dell’espressione (x != 0). Le due espressioni (x <= 3) e (x >= -3) hanno quindi la precedenza e un livello più basso, mentre il loro risultato è di pari livello rispetto a (x != 0). La funzione which ha anche una opzione molto importante, che si chiama arr.ind (contrazione di array indexes). Per assimilarla, facciamo un esempio riferito a una matrice
## [1] 3 3 1## [1] 3 3 1## [1] 6 7 8## row col
## [1,] 1 2
## [2,] 2 2
## [3,] 3 2L’utilizzo dell’opzione arr.ind non cambia il risultato dell’indicizzazione di x, ma cambia la forma in cui la funzione which ci restituisce gli indici di posizione degli elementi di x che soddisfano la condizione specificata. Se arr.ind disattiva, which tratta tutti gli oggetti (anche le matrici) come dei vettori, e dunque il risultato che ci fornisce è vettoriale. Se *arr.ind è attiva e stiamo lavorando su una matrice, which ci restituisce delle coordinate in due dimensioni: riga e colonna degli elementi di x che soddisfano la condizione desiderata.
4.13 L’uso dell’Help
Fino a questo punto, abbiamo subdolamente introdotto alcune funzioni di base di R (matrix, which, sum,…) illustrandone le principali caratteristiche. Queste e altre funzioni fanno parte del vocabolario di base che un neofita di R deve assimilare, ma ce ne sono tante altre che si aggiungono via via ed è evidente che dobbiamo capire come si fa ad apprendere il loro utilizzo (in maniera possibilmente rapida). La risposta è: usando l’help di R! L’Help di R è un interfaccia brutto e apparentemente antipatico. Però, a dispetto delle apparenze, è uno strumento estramemente versatile e completo, e quindi imparare a usarlo ci permette di procedere rapidamente con il nostro self training.
Per fare la sua conoscenza, proviamo a digitare da terminale il nome di una funzione preceduto dal punto interrogativo:
L’help di qualsiasi funzione di R è organizzato secondo le seguenti voci (per comodità ci riferiremo all’help della funzione matrix):
- Il nome della funzione: matrix {base}
- Il titolo dell’help: Matrices
- Una breve e concisa (occhio ai termini usati) descrizione della funzione: Description
- Un esempio generico ma completo del suo utilizzo: Usage
- Una dettagliata descrizione degli argomenti necessari e delle opzioni: Arguments
- Una articolata descrizione di cosa fa la funzione: Details
- Alcune annotazioni: Note
- I riferimenti alla letteratura (soprattutto se si tratta di una metodo scientifico): References
- Un elenco delle funzioni che sono “apparentate” con la nostra funzione: See Also
- Una serie di esempi pratici: Examples
Il nome della funzione (1) è sempre associato al nome del pacchetto, riportato tra parentesi graffe. Per adesso abbiamo incontrato solo funzione del pacchetto base, ma via via ne useremo molte altre disponibili mediante pacchetti aggiuntivi. Il titolo della funzione (2), da non confondere con il nome della funzione, è semplicemente una denominazione immediata ed esplicita di quello che la funzione serve a fare. La descrizione (3) è una breve frase, basata sull’utilizzo di termini precisi e con un chiaro significato nel contesto di R, di come lavora la funzione e di quello che ci consente di fare. La voce Usage (4) è probabilmente la più diretta, utile e efficare voce dell’help. Mano mano che si diventa esperti di R si impara a usare nuove funzioni scorrendo rapidamente il loro help e intuendone l’utilizzo proprio dalla voce usage. Essa ci indica immediatamente quali sono gli argomenti (gli input) necessari per far funzionare la funzione, ma ci dice anche si comporterà la funzione nel caso in cui non indichiamo esplicitamente alcuni argomenti. Ad esempio, nel caso della funzione matrix, ci dice che essa si aspetta 3 argomenti: data, nrow e ncol. Tuttavia, in assenza di indicazioni dell’utente, la funzione userà NA come valore di default dell’argomento data, e 1 come valore di nrow ed ncol. Vediamo tre esempi:
## [,1] [,2] [,3]
## [1,] NA NA NA
## [2,] NA NA NA
## [3,] NA NA NA## [,1]
## [1,] 1
## [2,] 2
## [3,] 3
## [4,] 4
## [5,] 5
## [6,] 6
## [7,] 7
## [8,] 8
## [9,] 9Nel primo caso otteniamo una matrice di 3 righe e 3 colonne piena di NA. Nel secondo caso abbiamo assegnato a data il vettore 1:9, quindi la funzione deve disporre 9 valori in qualche modo…. ma, essendo prioritario l’argomento nrow, la funzione genera un vettore colonna. Un aspetto importante è che ogni funzione di R si accontenta di avere i valori degli argomenti anche senza l’assegnazione al loro nome predefinito. Quindi se scriviamo:
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12R capirà che 1:9 è riferito a data, mentre 4 e 3 sono riferiti rispettivamente a nrow ed ncol. Quindi la voce usage ci dice anche in che ordine fornire gli argomenti alla funzione che ci interessa. Se vogliamo fornirli in ordine differente, però, (come può capitare con funzioni che hanno tanti argomenti) possiamo farlo usando nomi e assegnazioni. Ad esempio:
## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 10
## [3,] 3 7 11
## [4,] 4 8 12Ci fornisce lo stesso identico risultato di prima. La voce Arguments (5), comunque, ci può tornare utile se non abbiamo subito chiara la natura degli argomenti necessari, ad esempio di quale classe (vettore? matrice? lista?) essi devono essere. Allo stesso tempo, questa voce dell’help ci spieg bene a cosa servono le opzioni.
La voce Details (6) ci illustra il razionale della funzione, cioè quali procedure ci sono alla sua base, ma ci indica anche cosa attenderci in casi “particolari”. Nel caso della funzione matrix, la voce Details ci spiega che, quando la dimensione dell’argomento data non corrisponde al numero di celle della matrice, R prova ad “adattare i dati”, ad esempio riciclando gli elementi di data se sono meno di quelli attesi. Vediamo un esempio:
## Warning in matrix(data = 1:9, nrow = 4, ncol = 3): data length [9] is not a sub-
## multiple or multiple of the number of rows [4]## [,1] [,2] [,3]
## [1,] 1 5 9
## [2,] 2 6 1
## [3,] 3 7 2
## [4,] 4 8 3In questo caso abbiamo generato una matrice di 4 righe e 3 colonne, e quindi di 12 elementi, ma abbiamo fornito un vettore di soli 9 elementi come argomento data. Come si può intuire, R ha ricominciato da capo e dopo il 9 ha usato i valori 1, 2 e 3. Sulle voci Note, References e See Also non ci dilunghiamo perchè sono davvero molto intuitive.
4.14 Una cassetta degli attrezzi essenziali
In questa sezione faremo conoscenza, anche mediante alcuni esempi, con una seria di funzioni del pacchetto base di R. Conoscerle è utile per due motivi:
- ci permette di avere gli strumenti di base per cominciare a usare sul serio R
- ci allena ad apprendere in modo autonomo l’utilizzo di qualsiasi altra funzione.
Nella figura seguente sono rappresentate alcune delle funzioni del pacchetto base, arbitrariamente raggruppate sulla base di 7 diverse tipologie (tratteremo a parte le principali funzioni per fare grafici):
- Ramo Funzioni per generare oggetti
- Ramo Funzioni per esplorare gli oggetti
- Ramo Funzioni per la combinazione di oggetti
- Ramo Funzioni statistiche di base
- Ramo Funzioni per salvare i grafici
- Ramo Funzioni per leggere/salvare file di testo
- Ramo Funzioni per leggere/salvare dati nel formato R
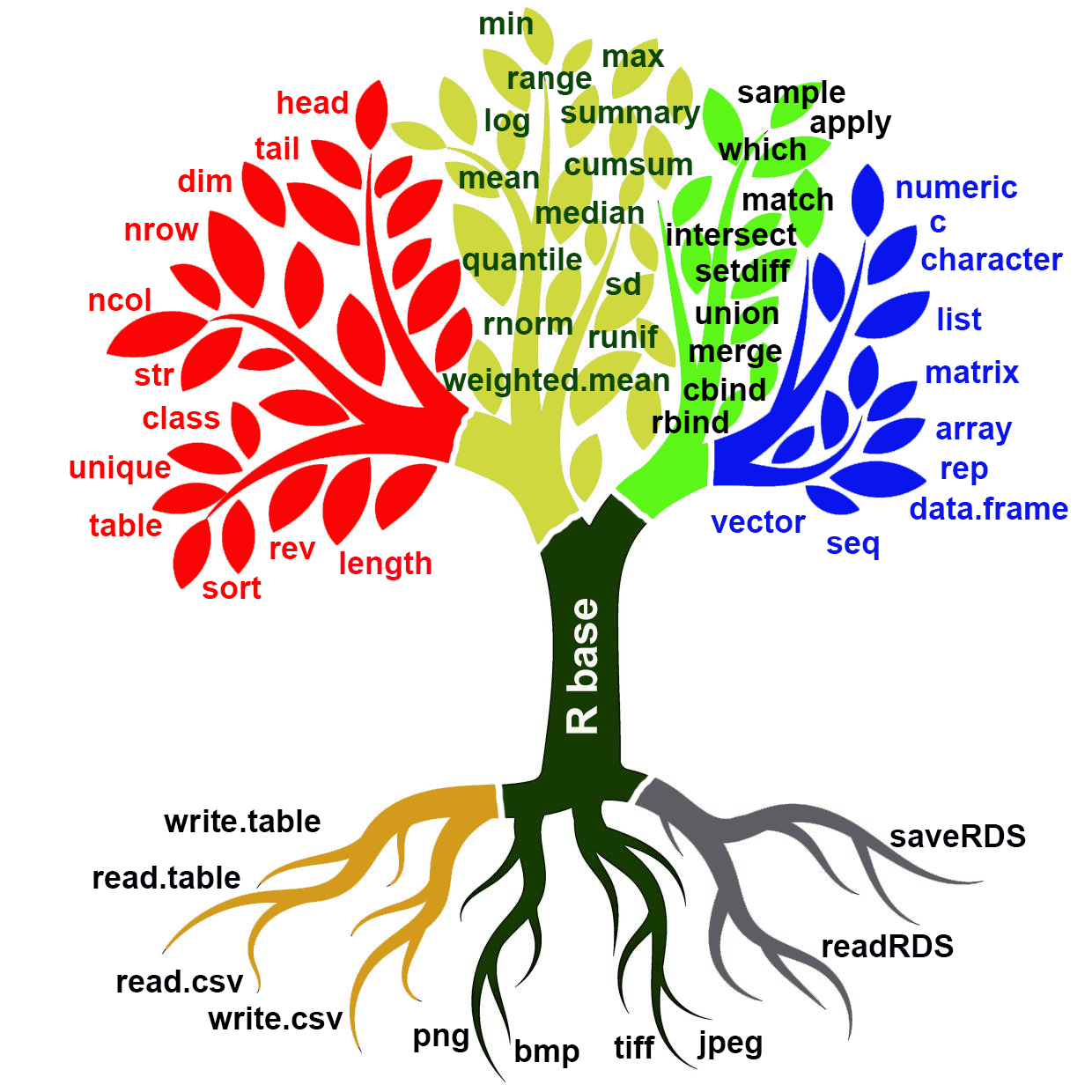Prendiamole in considerazione, illustrandone brevemente le caratteristiche e l’utilizzo.
4.14.1 c
E’ la funzione più semplice e infatti è una delle prima che abbiamo incontato. Gli input di questa funzione sono gli oggetti da unire per creare il vettore, e sono messi insieme nella stessa sequenza con cui vengono menzionati come argomenti. Serve a generare dei vettori che avranno, però, tutti gli oggetti appartenenti alla stessa classe. Questo vuol dire che, se forniamo a c argomenti di classi diverse, alcuni di loro saranno coerciti a diventare di classi diverse. Questo avviene secondo una logica intuitiva: se mescolo numeri e caratteri, avrò un vettore di solo caratteri (perchè non avrebbe senso trasformare i valori character in numeric).
## [1] "1" "2" "3" "A" "B"Invece ha senso convertire i livelli di un factor in una serie di valori ordinali
vector_factor = factor(c("a","b"), levels = c("a","b"))
vector_numeric = c(4:6)
c(vector_numeric, vector_factor)## [1] 4 5 6 1 2Infine, un factor mescolato a un character sarà prima convertito in numeric e poi in un carattere.
vector_factor = factor(c("a","b"), levels = c("a","b"))
vector_character = c("A","B")
c(vector_factor, vector_character)## [1] "1" "2" "A" "B"4.14.2 numeric
La funzione per creare vettore di numeri. L’argomento della funzione è la lunghezza del vettore che vogliamo generare. Indipendentemente dalla lunghezza, il vettore sarà costituito solo da zeri. Ha due cugini di cui as.numeric è spesso usato per coercire oggetti di classe diversa da numeric in vettori numerici. Se questa operazione non ha senso, la funzione as.numeric restituirà una serie di NA.
## [1] 0 0 0 0 0 0 0 0 0 0## [1] 0 0 0 0 0## [1] 1 2## Warning: si è prodotto un NA per coercizione## [1] NA NA4.14.3 character
Questa funzione si comporta esattamente come la funzione numeric: il suo unico argomento è la lunghezza del vettore di caratteri da generare, che sarà formato da stringhe vuote.
## [1] "" "" ""La funzione con essa imparentata, as.character, trasforma tutto quello che le si da come argomento in una seguenza di stringhe.
vector_factor = factor(c("a","b"), levels = c("a","b"))
vector_numeric = c(4:6)
as.character(vector_numeric)## [1] "4" "5" "6"## [1] "a" "b"4.14.4 list
Si tratta della funzione per assembrale delle liste, ed è molto semplice da usare: è sufficiente fornirle in input gli oggetti che formeranno gli elementi della lista. Si può decidere di nominarli oppure di non farlo, a seconda delle esigenze.
vector_factor = factor(c("a","b"), levels = c("a","b"))
vector_numeric = c(4:6)
vector_character = c("A","B")
list(vector_factor, vector_numeric, vector_character)## [[1]]
## [1] a b
## Levels: a b
##
## [[2]]
## [1] 4 5 6
##
## [[3]]
## [1] "A" "B"## $fattori
## [1] a b
## Levels: a b
##
## $numeri
## [1] 4 5 6
##
## $caratteri
## [1] "A" "B"4.14.5 matrix
Abbiamo già incontrato questa funzione. Essa vuole come argomenti obbligati la geometria della matrice da generare, in termini di numero di righe e numero di colonne, e il contenuto della matrice stessa (a meno che non ci accontentiamo che sia piena di NA). Come nel caso dei vettori, anche le matrice possono contenere solo oggetti che appartengono alla stessa classe.
## [,1] [,2] [,3]
## [1,] 1 4 7
## [2,] 2 5 8
## [3,] 3 6 9## Warning in matrix(c("a", "b", "c", "d", "e", "f", "g"), 3, 3): data length [7]
## is not a sub-multiple or multiple of the number of rows [3]## [,1] [,2] [,3]
## [1,] "a" "d" "g"
## [2,] "b" "e" "a"
## [3,] "c" "f" "b"## Warning in matrix(c("a", "b", "c", "d", 1, 2, 3), 3, 3): data length [7] is not
## a sub-multiple or multiple of the number of rows [3]## [,1] [,2] [,3]
## [1,] "a" "d" "3"
## [2,] "b" "1" "a"
## [3,] "c" "2" "b"Naturalmente sappiamo che dobbiamo prestare attenzione al modo in cui R riempirà la nostra matrice. Per questo dobbiamo ricordare che esiste la funzione byrow che ci permette di indicare se la matrice deve essere riempita per riga invece che per colonna. Un altro aspetto da considerare è la coerenza tra le dimensioni dell’argomento data e la geometria della matrice definita dai valori degli argomenti nrow e ncol. Se “i conti non tornano”, R cerca di farseli tornare ma ci avverte che qualcosa non va…
## Warning in matrix(1:9, 3, 4): data length [9] is not a sub-multiple or multiple
## of the number of columns [4]## [,1] [,2] [,3] [,4]
## [1,] 1 4 7 1
## [2,] 2 5 8 2
## [3,] 3 6 9 3In questo esempio, abbiamo messo R in imbarazzo dando alla funzione matrix argomenti discordanti: data è definito come un vettore di 9 elementi, ma i valori di nrow e ncol definiscono una matrice avente 12 celle! Come si vede, R “ricicla” gli elementi di data, ripartendo dall’inizio del vettore, ma ci avvisa con un warning. Tuttavia…
## [,1] [,2] [,3] [,4]
## [1,] 1 2 1 2
## [2,] 2 1 2 1
## [3,] 1 2 1 2In questo caso R non ha protestato, perchè replicando gli elementi di data è riuscito a ottenere un numero di elementi coerente con la geometria della matrice. Ovviamente questo è un caso particolare della regola generale:
## [,1] [,2] [,3] [,4]
## [1,] 100 100 100 100
## [2,] 100 100 100 100
## [3,] 100 100 100 100In questo caso, avendo assegnato all’argomento data un singolo valore numerico, qualsiasi geometria della matrice andrà bene.
4.14.6 array
Questa funzione è la corrispondente di matrix per matrici a n dimensioni con n che appartiene a N+. A parte l’argomento data, che è identico a quello di matrix, la funzione array vuole un argomento dim, nella forma di un vettore numerico in cui ogni valore specifica il numero di elementi corrispondente alla n-esima dimensione. Dunque il numero di dimensioni dipende dalla lunghezza del vettore associato a dim. Ad esempio
## , , 1
##
## [,1] [,2]
## [1,] 1 4
## [2,] 2 5
## [3,] 3 6
##
## , , 2
##
## [,1] [,2]
## [1,] 7 10
## [2,] 8 11
## [3,] 9 12
##
## , , 3
##
## [,1] [,2]
## [1,] 13 16
## [2,] 14 17
## [3,] 15 18
##
## , , 4
##
## [,1] [,2]
## [1,] 19 22
## [2,] 20 23
## [3,] 21 24E’ interessante fare la conoscenza con il modo, rozzo ma efficace, che R usa per mostrarci oggetti compessi come questo array a 3 dimensioni. Per orientarsi, si devono utilizzare gli indici, tra quadre, che ci indicano quale strato dell’array ci viene mostrato. Essendo alle prese con un array tridimensionale, ci servono 3 coordinate per identificare un suo elemento, e quindi tra le quadre (che servono per indicizzarlo) vediamo 2 virgole che separano 3 valori, siano essi presenti o meno. Quindi la scrittura [,2,3] vuol dire prendi TUTTI gli elementi dell’array rispetto alla sua prima dimensione, solo il secondo rispetto alla seconda dimensione e solo il terzo rispetto alla terza dimensione. Chiaro no?
## [1] 16 17 184.14.7 data.frame
I data frame sono sicuramente gli oggetti più flessibili di R, e sono di gran lunga il tipo più usato per organizzare, gestire e analizzare dati biologici. I data frame combinano la “rigidità” strutturale delle matrici (ogni riga di un data frame ha le stesse colonne di ogni altra, e viceversa per le colonne) con la flessibilità del poter incorporare dati factor, numeric, character, ecc. Questo vuol dire che, generalmente, le colonne di un data frame contengono record (righe) omogenei e, quindi, ogni variabile (colonna) è formata da valori che appartengono alla stessa classe di R. Questo, però, li rende oggetti non ideali per fare calcoli, come vedremo parlando delle funzioni matematico-statistiche. Per fare pratica coi data frame introduciamo uno dei dataset nativi del pacchetto base di R, il data frame iris
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
## 7 4.6 3.4 1.4 0.3 setosa
## 8 5.0 3.4 1.5 0.2 setosa
## 9 4.4 2.9 1.4 0.2 setosa
## 10 4.9 3.1 1.5 0.1 setosa
## 11 5.4 3.7 1.5 0.2 setosa
## 12 4.8 3.4 1.6 0.2 setosa
## 13 4.8 3.0 1.4 0.1 setosa
## 14 4.3 3.0 1.1 0.1 setosa
## 15 5.8 4.0 1.2 0.2 setosa
## 16 5.7 4.4 1.5 0.4 setosa
## 17 5.4 3.9 1.3 0.4 setosa
## 18 5.1 3.5 1.4 0.3 setosa
## 19 5.7 3.8 1.7 0.3 setosa
## 20 5.1 3.8 1.5 0.3 setosa
## 21 5.4 3.4 1.7 0.2 setosa
## 22 5.1 3.7 1.5 0.4 setosa
## 23 4.6 3.6 1.0 0.2 setosa
## 24 5.1 3.3 1.7 0.5 setosa
## 25 4.8 3.4 1.9 0.2 setosa
## 26 5.0 3.0 1.6 0.2 setosa
## 27 5.0 3.4 1.6 0.4 setosa
## 28 5.2 3.5 1.5 0.2 setosa
## 29 5.2 3.4 1.4 0.2 setosa
## 30 4.7 3.2 1.6 0.2 setosa
## 31 4.8 3.1 1.6 0.2 setosa
## 32 5.4 3.4 1.5 0.4 setosa
## 33 5.2 4.1 1.5 0.1 setosa
## 34 5.5 4.2 1.4 0.2 setosa
## 35 4.9 3.1 1.5 0.2 setosa
## 36 5.0 3.2 1.2 0.2 setosa
## 37 5.5 3.5 1.3 0.2 setosa
## 38 4.9 3.6 1.4 0.1 setosa
## 39 4.4 3.0 1.3 0.2 setosa
## 40 5.1 3.4 1.5 0.2 setosa
## 41 5.0 3.5 1.3 0.3 setosa
## 42 4.5 2.3 1.3 0.3 setosa
## 43 4.4 3.2 1.3 0.2 setosa
## 44 5.0 3.5 1.6 0.6 setosa
## 45 5.1 3.8 1.9 0.4 setosa
## 46 4.8 3.0 1.4 0.3 setosa
## 47 5.1 3.8 1.6 0.2 setosa
## 48 4.6 3.2 1.4 0.2 setosa
## 49 5.3 3.7 1.5 0.2 setosa
## 50 5.0 3.3 1.4 0.2 setosa
## 51 7.0 3.2 4.7 1.4 versicolor
## 52 6.4 3.2 4.5 1.5 versicolor
## 53 6.9 3.1 4.9 1.5 versicolor
## 54 5.5 2.3 4.0 1.3 versicolor
## 55 6.5 2.8 4.6 1.5 versicolor
## 56 5.7 2.8 4.5 1.3 versicolor
## 57 6.3 3.3 4.7 1.6 versicolor
## 58 4.9 2.4 3.3 1.0 versicolor
## 59 6.6 2.9 4.6 1.3 versicolor
## 60 5.2 2.7 3.9 1.4 versicolor
## 61 5.0 2.0 3.5 1.0 versicolor
## 62 5.9 3.0 4.2 1.5 versicolor
## 63 6.0 2.2 4.0 1.0 versicolor
## 64 6.1 2.9 4.7 1.4 versicolor
## 65 5.6 2.9 3.6 1.3 versicolor
## 66 6.7 3.1 4.4 1.4 versicolor
## 67 5.6 3.0 4.5 1.5 versicolor
## 68 5.8 2.7 4.1 1.0 versicolor
## 69 6.2 2.2 4.5 1.5 versicolor
## 70 5.6 2.5 3.9 1.1 versicolor
## 71 5.9 3.2 4.8 1.8 versicolor
## 72 6.1 2.8 4.0 1.3 versicolor
## 73 6.3 2.5 4.9 1.5 versicolor
## 74 6.1 2.8 4.7 1.2 versicolor
## 75 6.4 2.9 4.3 1.3 versicolor
## 76 6.6 3.0 4.4 1.4 versicolor
## 77 6.8 2.8 4.8 1.4 versicolor
## 78 6.7 3.0 5.0 1.7 versicolor
## 79 6.0 2.9 4.5 1.5 versicolor
## 80 5.7 2.6 3.5 1.0 versicolor
## 81 5.5 2.4 3.8 1.1 versicolor
## 82 5.5 2.4 3.7 1.0 versicolor
## 83 5.8 2.7 3.9 1.2 versicolor
## 84 6.0 2.7 5.1 1.6 versicolor
## 85 5.4 3.0 4.5 1.5 versicolor
## 86 6.0 3.4 4.5 1.6 versicolor
## 87 6.7 3.1 4.7 1.5 versicolor
## 88 6.3 2.3 4.4 1.3 versicolor
## 89 5.6 3.0 4.1 1.3 versicolor
## 90 5.5 2.5 4.0 1.3 versicolor
## 91 5.5 2.6 4.4 1.2 versicolor
## 92 6.1 3.0 4.6 1.4 versicolor
## 93 5.8 2.6 4.0 1.2 versicolor
## 94 5.0 2.3 3.3 1.0 versicolor
## 95 5.6 2.7 4.2 1.3 versicolor
## 96 5.7 3.0 4.2 1.2 versicolor
## 97 5.7 2.9 4.2 1.3 versicolor
## 98 6.2 2.9 4.3 1.3 versicolor
## 99 5.1 2.5 3.0 1.1 versicolor
## 100 5.7 2.8 4.1 1.3 versicolor
## 101 6.3 3.3 6.0 2.5 virginica
## 102 5.8 2.7 5.1 1.9 virginica
## 103 7.1 3.0 5.9 2.1 virginica
## 104 6.3 2.9 5.6 1.8 virginica
## 105 6.5 3.0 5.8 2.2 virginica
## 106 7.6 3.0 6.6 2.1 virginica
## 107 4.9 2.5 4.5 1.7 virginica
## 108 7.3 2.9 6.3 1.8 virginica
## 109 6.7 2.5 5.8 1.8 virginica
## 110 7.2 3.6 6.1 2.5 virginica
## 111 6.5 3.2 5.1 2.0 virginica
## 112 6.4 2.7 5.3 1.9 virginica
## 113 6.8 3.0 5.5 2.1 virginica
## 114 5.7 2.5 5.0 2.0 virginica
## 115 5.8 2.8 5.1 2.4 virginica
## 116 6.4 3.2 5.3 2.3 virginica
## 117 6.5 3.0 5.5 1.8 virginica
## 118 7.7 3.8 6.7 2.2 virginica
## 119 7.7 2.6 6.9 2.3 virginica
## 120 6.0 2.2 5.0 1.5 virginica
## 121 6.9 3.2 5.7 2.3 virginica
## 122 5.6 2.8 4.9 2.0 virginica
## 123 7.7 2.8 6.7 2.0 virginica
## 124 6.3 2.7 4.9 1.8 virginica
## 125 6.7 3.3 5.7 2.1 virginica
## 126 7.2 3.2 6.0 1.8 virginica
## 127 6.2 2.8 4.8 1.8 virginica
## 128 6.1 3.0 4.9 1.8 virginica
## 129 6.4 2.8 5.6 2.1 virginica
## 130 7.2 3.0 5.8 1.6 virginica
## 131 7.4 2.8 6.1 1.9 virginica
## 132 7.9 3.8 6.4 2.0 virginica
## 133 6.4 2.8 5.6 2.2 virginica
## 134 6.3 2.8 5.1 1.5 virginica
## 135 6.1 2.6 5.6 1.4 virginica
## 136 7.7 3.0 6.1 2.3 virginica
## 137 6.3 3.4 5.6 2.4 virginica
## 138 6.4 3.1 5.5 1.8 virginica
## 139 6.0 3.0 4.8 1.8 virginica
## 140 6.9 3.1 5.4 2.1 virginica
## 141 6.7 3.1 5.6 2.4 virginica
## 142 6.9 3.1 5.1 2.3 virginica
## 143 5.8 2.7 5.1 1.9 virginica
## 144 6.8 3.2 5.9 2.3 virginica
## 145 6.7 3.3 5.7 2.5 virginica
## 146 6.7 3.0 5.2 2.3 virginica
## 147 6.3 2.5 5.0 1.9 virginica
## 148 6.5 3.0 5.2 2.0 virginica
## 149 6.2 3.4 5.4 2.3 virginica
## 150 5.9 3.0 5.1 1.8 virginicaIris è un famoso insieme di dati (Fisher’s or Anderson’s) che contiene biometrie di individui (fiori) di 3 specie del genere Iris. Come si può notare, ogni colonna ha un nome che corrisponde alla biometria misurata, mentre l’ultima colonna è un factor con 3 livelli corrispondenti alle 3 specie. Nel caso dei data frame, oltre alla normale indicizizzazione basata sulle parentesi quadre, possiamo disporre di un riferimento diretto alle colonne (variabili) mediante il simbolo $. Ad esempio
## [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
## [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
## [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
## [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
## [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
## [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
## [109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
## [127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
## [145] 6.7 6.7 6.3 6.5 6.2 5.9## [1] setosa setosa setosa setosa setosa setosa
## [7] setosa setosa setosa setosa setosa setosa
## [13] setosa setosa setosa setosa setosa setosa
## [19] setosa setosa setosa setosa setosa setosa
## [25] setosa setosa setosa setosa setosa setosa
## [31] setosa setosa setosa setosa setosa setosa
## [37] setosa setosa setosa setosa setosa setosa
## [43] setosa setosa setosa setosa setosa setosa
## [49] setosa setosa versicolor versicolor versicolor versicolor
## [55] versicolor versicolor versicolor versicolor versicolor versicolor
## [61] versicolor versicolor versicolor versicolor versicolor versicolor
## [67] versicolor versicolor versicolor versicolor versicolor versicolor
## [73] versicolor versicolor versicolor versicolor versicolor versicolor
## [79] versicolor versicolor versicolor versicolor versicolor versicolor
## [85] versicolor versicolor versicolor versicolor versicolor versicolor
## [91] versicolor versicolor versicolor versicolor versicolor versicolor
## [97] versicolor versicolor versicolor versicolor virginica virginica
## [103] virginica virginica virginica virginica virginica virginica
## [109] virginica virginica virginica virginica virginica virginica
## [115] virginica virginica virginica virginica virginica virginica
## [121] virginica virginica virginica virginica virginica virginica
## [127] virginica virginica virginica virginica virginica virginica
## [133] virginica virginica virginica virginica virginica virginica
## [139] virginica virginica virginica virginica virginica virginica
## [145] virginica virginica virginica virginica virginica virginica
## Levels: setosa versicolor virginicaQuindi, usando il comando class, possiamo esaminare ogni variabile.
## [1] "numeric"## [1] "numeric"## [1] "numeric"## [1] "numeric"## [1] "factor"Esistono due modi in cui si può organizzare un data frame. Il primo, detto wide, contiene osservazioni ripetute di un soggetto in una singola riga, e ogni risposta è in una colonna separata. Il data frame iris è un esempio di data frame wide. Nel secondo tipo, detto long, ogni riga è combinazione di soggetto e risposta (variabile) su di esso osservata. Il data frame iris nel formato long ci appare così:
## Warning: attributes are not identical across measure variables; they will be
## dropped## id variable value
## 1 1 Sepal.Length 5.1
## 2 2 Sepal.Length 4.9
## 3 3 Sepal.Length 4.7
## 4 4 Sepal.Length 4.6
## 5 5 Sepal.Length 5
## 6 6 Sepal.Length 5.4
## 7 7 Sepal.Length 4.6
## 8 8 Sepal.Length 5
## 9 9 Sepal.Length 4.4
## 10 10 Sepal.Length 4.9
## 11 11 Sepal.Length 5.4
## 12 12 Sepal.Length 4.8
## 13 13 Sepal.Length 4.8
## 14 14 Sepal.Length 4.3
## 15 15 Sepal.Length 5.8
## 16 16 Sepal.Length 5.7
## 17 17 Sepal.Length 5.4
## 18 18 Sepal.Length 5.1
## 19 19 Sepal.Length 5.7
## 20 20 Sepal.Length 5.1
## 21 21 Sepal.Length 5.4
## 22 22 Sepal.Length 5.1
## 23 23 Sepal.Length 4.6
## 24 24 Sepal.Length 5.1
## 25 25 Sepal.Length 4.8
## 26 26 Sepal.Length 5
## 27 27 Sepal.Length 5
## 28 28 Sepal.Length 5.2
## 29 29 Sepal.Length 5.2
## 30 30 Sepal.Length 4.7
## 31 31 Sepal.Length 4.8
## 32 32 Sepal.Length 5.4
## 33 33 Sepal.Length 5.2
## 34 34 Sepal.Length 5.5
## 35 35 Sepal.Length 4.9
## 36 36 Sepal.Length 5
## 37 37 Sepal.Length 5.5
## 38 38 Sepal.Length 4.9
## 39 39 Sepal.Length 4.4
## 40 40 Sepal.Length 5.1
## 41 41 Sepal.Length 5
## 42 42 Sepal.Length 4.5
## 43 43 Sepal.Length 4.4
## 44 44 Sepal.Length 5
## 45 45 Sepal.Length 5.1
## 46 46 Sepal.Length 4.8
## 47 47 Sepal.Length 5.1
## 48 48 Sepal.Length 4.6
## 49 49 Sepal.Length 5.3
## 50 50 Sepal.Length 5
## 51 51 Sepal.Length 7
## 52 52 Sepal.Length 6.4
## 53 53 Sepal.Length 6.9
## 54 54 Sepal.Length 5.5
## 55 55 Sepal.Length 6.5
## 56 56 Sepal.Length 5.7
## 57 57 Sepal.Length 6.3
## 58 58 Sepal.Length 4.9
## 59 59 Sepal.Length 6.6
## 60 60 Sepal.Length 5.2
## 61 61 Sepal.Length 5
## 62 62 Sepal.Length 5.9
## 63 63 Sepal.Length 6
## 64 64 Sepal.Length 6.1
## 65 65 Sepal.Length 5.6
## 66 66 Sepal.Length 6.7
## 67 67 Sepal.Length 5.6
## 68 68 Sepal.Length 5.8
## 69 69 Sepal.Length 6.2
## 70 70 Sepal.Length 5.6
## 71 71 Sepal.Length 5.9
## 72 72 Sepal.Length 6.1
## 73 73 Sepal.Length 6.3
## 74 74 Sepal.Length 6.1
## 75 75 Sepal.Length 6.4
## 76 76 Sepal.Length 6.6
## 77 77 Sepal.Length 6.8
## 78 78 Sepal.Length 6.7
## 79 79 Sepal.Length 6
## 80 80 Sepal.Length 5.7
## 81 81 Sepal.Length 5.5
## 82 82 Sepal.Length 5.5
## 83 83 Sepal.Length 5.8
## 84 84 Sepal.Length 6
## 85 85 Sepal.Length 5.4
## 86 86 Sepal.Length 6
## 87 87 Sepal.Length 6.7
## 88 88 Sepal.Length 6.3
## 89 89 Sepal.Length 5.6
## 90 90 Sepal.Length 5.5
## 91 91 Sepal.Length 5.5
## 92 92 Sepal.Length 6.1
## 93 93 Sepal.Length 5.8
## 94 94 Sepal.Length 5
## 95 95 Sepal.Length 5.6
## 96 96 Sepal.Length 5.7
## 97 97 Sepal.Length 5.7
## 98 98 Sepal.Length 6.2
## 99 99 Sepal.Length 5.1
## 100 100 Sepal.Length 5.7
## 101 101 Sepal.Length 6.3
## 102 102 Sepal.Length 5.8
## 103 103 Sepal.Length 7.1
## 104 104 Sepal.Length 6.3
## 105 105 Sepal.Length 6.5
## 106 106 Sepal.Length 7.6
## 107 107 Sepal.Length 4.9
## 108 108 Sepal.Length 7.3
## 109 109 Sepal.Length 6.7
## 110 110 Sepal.Length 7.2
## 111 111 Sepal.Length 6.5
## 112 112 Sepal.Length 6.4
## 113 113 Sepal.Length 6.8
## 114 114 Sepal.Length 5.7
## 115 115 Sepal.Length 5.8
## 116 116 Sepal.Length 6.4
## 117 117 Sepal.Length 6.5
## 118 118 Sepal.Length 7.7
## 119 119 Sepal.Length 7.7
## 120 120 Sepal.Length 6
## 121 121 Sepal.Length 6.9
## 122 122 Sepal.Length 5.6
## 123 123 Sepal.Length 7.7
## 124 124 Sepal.Length 6.3
## 125 125 Sepal.Length 6.7
## 126 126 Sepal.Length 7.2
## 127 127 Sepal.Length 6.2
## 128 128 Sepal.Length 6.1
## 129 129 Sepal.Length 6.4
## 130 130 Sepal.Length 7.2
## 131 131 Sepal.Length 7.4
## 132 132 Sepal.Length 7.9
## 133 133 Sepal.Length 6.4
## 134 134 Sepal.Length 6.3
## 135 135 Sepal.Length 6.1
## 136 136 Sepal.Length 7.7
## 137 137 Sepal.Length 6.3
## 138 138 Sepal.Length 6.4
## 139 139 Sepal.Length 6
## 140 140 Sepal.Length 6.9
## 141 141 Sepal.Length 6.7
## 142 142 Sepal.Length 6.9
## 143 143 Sepal.Length 5.8
## 144 144 Sepal.Length 6.8
## 145 145 Sepal.Length 6.7
## 146 146 Sepal.Length 6.7
## 147 147 Sepal.Length 6.3
## 148 148 Sepal.Length 6.5
## 149 149 Sepal.Length 6.2
## 150 150 Sepal.Length 5.9
## 151 1 Sepal.Width 3.5
## 152 2 Sepal.Width 3
## 153 3 Sepal.Width 3.2
## 154 4 Sepal.Width 3.1
## 155 5 Sepal.Width 3.6
## 156 6 Sepal.Width 3.9
## 157 7 Sepal.Width 3.4
## 158 8 Sepal.Width 3.4
## 159 9 Sepal.Width 2.9
## 160 10 Sepal.Width 3.1
## 161 11 Sepal.Width 3.7
## 162 12 Sepal.Width 3.4
## 163 13 Sepal.Width 3
## 164 14 Sepal.Width 3
## 165 15 Sepal.Width 4
## 166 16 Sepal.Width 4.4
## 167 17 Sepal.Width 3.9
## 168 18 Sepal.Width 3.5
## 169 19 Sepal.Width 3.8
## 170 20 Sepal.Width 3.8
## 171 21 Sepal.Width 3.4
## 172 22 Sepal.Width 3.7
## 173 23 Sepal.Width 3.6
## 174 24 Sepal.Width 3.3
## 175 25 Sepal.Width 3.4
## 176 26 Sepal.Width 3
## 177 27 Sepal.Width 3.4
## 178 28 Sepal.Width 3.5
## 179 29 Sepal.Width 3.4
## 180 30 Sepal.Width 3.2
## 181 31 Sepal.Width 3.1
## 182 32 Sepal.Width 3.4
## 183 33 Sepal.Width 4.1
## 184 34 Sepal.Width 4.2
## 185 35 Sepal.Width 3.1
## 186 36 Sepal.Width 3.2
## 187 37 Sepal.Width 3.5
## 188 38 Sepal.Width 3.6
## 189 39 Sepal.Width 3
## 190 40 Sepal.Width 3.4
## 191 41 Sepal.Width 3.5
## 192 42 Sepal.Width 2.3
## 193 43 Sepal.Width 3.2
## 194 44 Sepal.Width 3.5
## 195 45 Sepal.Width 3.8
## 196 46 Sepal.Width 3
## 197 47 Sepal.Width 3.8
## 198 48 Sepal.Width 3.2
## 199 49 Sepal.Width 3.7
## 200 50 Sepal.Width 3.3
## 201 51 Sepal.Width 3.2
## 202 52 Sepal.Width 3.2
## 203 53 Sepal.Width 3.1
## 204 54 Sepal.Width 2.3
## 205 55 Sepal.Width 2.8
## 206 56 Sepal.Width 2.8
## 207 57 Sepal.Width 3.3
## 208 58 Sepal.Width 2.4
## 209 59 Sepal.Width 2.9
## 210 60 Sepal.Width 2.7
## 211 61 Sepal.Width 2
## 212 62 Sepal.Width 3
## 213 63 Sepal.Width 2.2
## 214 64 Sepal.Width 2.9
## 215 65 Sepal.Width 2.9
## 216 66 Sepal.Width 3.1
## 217 67 Sepal.Width 3
## 218 68 Sepal.Width 2.7
## 219 69 Sepal.Width 2.2
## 220 70 Sepal.Width 2.5
## 221 71 Sepal.Width 3.2
## 222 72 Sepal.Width 2.8
## 223 73 Sepal.Width 2.5
## 224 74 Sepal.Width 2.8
## 225 75 Sepal.Width 2.9
## 226 76 Sepal.Width 3
## 227 77 Sepal.Width 2.8
## 228 78 Sepal.Width 3
## 229 79 Sepal.Width 2.9
## 230 80 Sepal.Width 2.6
## 231 81 Sepal.Width 2.4
## 232 82 Sepal.Width 2.4
## 233 83 Sepal.Width 2.7
## 234 84 Sepal.Width 2.7
## 235 85 Sepal.Width 3
## 236 86 Sepal.Width 3.4
## 237 87 Sepal.Width 3.1
## 238 88 Sepal.Width 2.3
## 239 89 Sepal.Width 3
## 240 90 Sepal.Width 2.5
## 241 91 Sepal.Width 2.6
## 242 92 Sepal.Width 3
## 243 93 Sepal.Width 2.6
## 244 94 Sepal.Width 2.3
## 245 95 Sepal.Width 2.7
## 246 96 Sepal.Width 3
## 247 97 Sepal.Width 2.9
## 248 98 Sepal.Width 2.9
## 249 99 Sepal.Width 2.5
## 250 100 Sepal.Width 2.8
## 251 101 Sepal.Width 3.3
## 252 102 Sepal.Width 2.7
## 253 103 Sepal.Width 3
## 254 104 Sepal.Width 2.9
## 255 105 Sepal.Width 3
## 256 106 Sepal.Width 3
## 257 107 Sepal.Width 2.5
## 258 108 Sepal.Width 2.9
## 259 109 Sepal.Width 2.5
## 260 110 Sepal.Width 3.6
## 261 111 Sepal.Width 3.2
## 262 112 Sepal.Width 2.7
## 263 113 Sepal.Width 3
## 264 114 Sepal.Width 2.5
## 265 115 Sepal.Width 2.8
## 266 116 Sepal.Width 3.2
## 267 117 Sepal.Width 3
## 268 118 Sepal.Width 3.8
## 269 119 Sepal.Width 2.6
## 270 120 Sepal.Width 2.2
## 271 121 Sepal.Width 3.2
## 272 122 Sepal.Width 2.8
## 273 123 Sepal.Width 2.8
## 274 124 Sepal.Width 2.7
## 275 125 Sepal.Width 3.3
## 276 126 Sepal.Width 3.2
## 277 127 Sepal.Width 2.8
## 278 128 Sepal.Width 3
## 279 129 Sepal.Width 2.8
## 280 130 Sepal.Width 3
## 281 131 Sepal.Width 2.8
## 282 132 Sepal.Width 3.8
## 283 133 Sepal.Width 2.8
## 284 134 Sepal.Width 2.8
## 285 135 Sepal.Width 2.6
## 286 136 Sepal.Width 3
## 287 137 Sepal.Width 3.4
## 288 138 Sepal.Width 3.1
## 289 139 Sepal.Width 3
## 290 140 Sepal.Width 3.1
## 291 141 Sepal.Width 3.1
## 292 142 Sepal.Width 3.1
## 293 143 Sepal.Width 2.7
## 294 144 Sepal.Width 3.2
## 295 145 Sepal.Width 3.3
## 296 146 Sepal.Width 3
## 297 147 Sepal.Width 2.5
## 298 148 Sepal.Width 3
## 299 149 Sepal.Width 3.4
## 300 150 Sepal.Width 3
## 301 1 Petal.Length 1.4
## 302 2 Petal.Length 1.4
## 303 3 Petal.Length 1.3
## 304 4 Petal.Length 1.5
## 305 5 Petal.Length 1.4
## 306 6 Petal.Length 1.7
## 307 7 Petal.Length 1.4
## 308 8 Petal.Length 1.5
## 309 9 Petal.Length 1.4
## 310 10 Petal.Length 1.5
## 311 11 Petal.Length 1.5
## 312 12 Petal.Length 1.6
## 313 13 Petal.Length 1.4
## 314 14 Petal.Length 1.1
## 315 15 Petal.Length 1.2
## 316 16 Petal.Length 1.5
## 317 17 Petal.Length 1.3
## 318 18 Petal.Length 1.4
## 319 19 Petal.Length 1.7
## 320 20 Petal.Length 1.5
## 321 21 Petal.Length 1.7
## 322 22 Petal.Length 1.5
## 323 23 Petal.Length 1
## 324 24 Petal.Length 1.7
## 325 25 Petal.Length 1.9
## 326 26 Petal.Length 1.6
## 327 27 Petal.Length 1.6
## 328 28 Petal.Length 1.5
## 329 29 Petal.Length 1.4
## 330 30 Petal.Length 1.6
## 331 31 Petal.Length 1.6
## 332 32 Petal.Length 1.5
## 333 33 Petal.Length 1.5
## 334 34 Petal.Length 1.4
## 335 35 Petal.Length 1.5
## 336 36 Petal.Length 1.2
## 337 37 Petal.Length 1.3
## 338 38 Petal.Length 1.4
## 339 39 Petal.Length 1.3
## 340 40 Petal.Length 1.5
## 341 41 Petal.Length 1.3
## 342 42 Petal.Length 1.3
## 343 43 Petal.Length 1.3
## 344 44 Petal.Length 1.6
## 345 45 Petal.Length 1.9
## 346 46 Petal.Length 1.4
## 347 47 Petal.Length 1.6
## 348 48 Petal.Length 1.4
## 349 49 Petal.Length 1.5
## 350 50 Petal.Length 1.4
## 351 51 Petal.Length 4.7
## 352 52 Petal.Length 4.5
## 353 53 Petal.Length 4.9
## 354 54 Petal.Length 4
## 355 55 Petal.Length 4.6
## 356 56 Petal.Length 4.5
## 357 57 Petal.Length 4.7
## 358 58 Petal.Length 3.3
## 359 59 Petal.Length 4.6
## 360 60 Petal.Length 3.9
## 361 61 Petal.Length 3.5
## 362 62 Petal.Length 4.2
## 363 63 Petal.Length 4
## 364 64 Petal.Length 4.7
## 365 65 Petal.Length 3.6
## 366 66 Petal.Length 4.4
## 367 67 Petal.Length 4.5
## 368 68 Petal.Length 4.1
## 369 69 Petal.Length 4.5
## 370 70 Petal.Length 3.9
## 371 71 Petal.Length 4.8
## 372 72 Petal.Length 4
## 373 73 Petal.Length 4.9
## 374 74 Petal.Length 4.7
## 375 75 Petal.Length 4.3
## 376 76 Petal.Length 4.4
## 377 77 Petal.Length 4.8
## 378 78 Petal.Length 5
## 379 79 Petal.Length 4.5
## 380 80 Petal.Length 3.5
## 381 81 Petal.Length 3.8
## 382 82 Petal.Length 3.7
## 383 83 Petal.Length 3.9
## 384 84 Petal.Length 5.1
## 385 85 Petal.Length 4.5
## 386 86 Petal.Length 4.5
## 387 87 Petal.Length 4.7
## 388 88 Petal.Length 4.4
## 389 89 Petal.Length 4.1
## 390 90 Petal.Length 4
## 391 91 Petal.Length 4.4
## 392 92 Petal.Length 4.6
## 393 93 Petal.Length 4
## 394 94 Petal.Length 3.3
## 395 95 Petal.Length 4.2
## 396 96 Petal.Length 4.2
## 397 97 Petal.Length 4.2
## 398 98 Petal.Length 4.3
## 399 99 Petal.Length 3
## 400 100 Petal.Length 4.1
## 401 101 Petal.Length 6
## 402 102 Petal.Length 5.1
## 403 103 Petal.Length 5.9
## 404 104 Petal.Length 5.6
## 405 105 Petal.Length 5.8
## 406 106 Petal.Length 6.6
## 407 107 Petal.Length 4.5
## 408 108 Petal.Length 6.3
## 409 109 Petal.Length 5.8
## 410 110 Petal.Length 6.1
## 411 111 Petal.Length 5.1
## 412 112 Petal.Length 5.3
## 413 113 Petal.Length 5.5
## 414 114 Petal.Length 5
## 415 115 Petal.Length 5.1
## 416 116 Petal.Length 5.3
## 417 117 Petal.Length 5.5
## 418 118 Petal.Length 6.7
## 419 119 Petal.Length 6.9
## 420 120 Petal.Length 5
## 421 121 Petal.Length 5.7
## 422 122 Petal.Length 4.9
## 423 123 Petal.Length 6.7
## 424 124 Petal.Length 4.9
## 425 125 Petal.Length 5.7
## 426 126 Petal.Length 6
## 427 127 Petal.Length 4.8
## 428 128 Petal.Length 4.9
## 429 129 Petal.Length 5.6
## 430 130 Petal.Length 5.8
## 431 131 Petal.Length 6.1
## 432 132 Petal.Length 6.4
## 433 133 Petal.Length 5.6
## 434 134 Petal.Length 5.1
## 435 135 Petal.Length 5.6
## 436 136 Petal.Length 6.1
## 437 137 Petal.Length 5.6
## 438 138 Petal.Length 5.5
## 439 139 Petal.Length 4.8
## 440 140 Petal.Length 5.4
## 441 141 Petal.Length 5.6
## 442 142 Petal.Length 5.1
## 443 143 Petal.Length 5.1
## 444 144 Petal.Length 5.9
## 445 145 Petal.Length 5.7
## 446 146 Petal.Length 5.2
## 447 147 Petal.Length 5
## 448 148 Petal.Length 5.2
## 449 149 Petal.Length 5.4
## 450 150 Petal.Length 5.1
## 451 1 Petal.Width 0.2
## 452 2 Petal.Width 0.2
## 453 3 Petal.Width 0.2
## 454 4 Petal.Width 0.2
## 455 5 Petal.Width 0.2
## 456 6 Petal.Width 0.4
## 457 7 Petal.Width 0.3
## 458 8 Petal.Width 0.2
## 459 9 Petal.Width 0.2
## 460 10 Petal.Width 0.1
## 461 11 Petal.Width 0.2
## 462 12 Petal.Width 0.2
## 463 13 Petal.Width 0.1
## 464 14 Petal.Width 0.1
## 465 15 Petal.Width 0.2
## 466 16 Petal.Width 0.4
## 467 17 Petal.Width 0.4
## 468 18 Petal.Width 0.3
## 469 19 Petal.Width 0.3
## 470 20 Petal.Width 0.3
## 471 21 Petal.Width 0.2
## 472 22 Petal.Width 0.4
## 473 23 Petal.Width 0.2
## 474 24 Petal.Width 0.5
## 475 25 Petal.Width 0.2
## 476 26 Petal.Width 0.2
## 477 27 Petal.Width 0.4
## 478 28 Petal.Width 0.2
## 479 29 Petal.Width 0.2
## 480 30 Petal.Width 0.2
## 481 31 Petal.Width 0.2
## 482 32 Petal.Width 0.4
## 483 33 Petal.Width 0.1
## 484 34 Petal.Width 0.2
## 485 35 Petal.Width 0.2
## 486 36 Petal.Width 0.2
## 487 37 Petal.Width 0.2
## 488 38 Petal.Width 0.1
## 489 39 Petal.Width 0.2
## 490 40 Petal.Width 0.2
## 491 41 Petal.Width 0.3
## 492 42 Petal.Width 0.3
## 493 43 Petal.Width 0.2
## 494 44 Petal.Width 0.6
## 495 45 Petal.Width 0.4
## 496 46 Petal.Width 0.3
## 497 47 Petal.Width 0.2
## 498 48 Petal.Width 0.2
## 499 49 Petal.Width 0.2
## 500 50 Petal.Width 0.2
## 501 51 Petal.Width 1.4
## 502 52 Petal.Width 1.5
## 503 53 Petal.Width 1.5
## 504 54 Petal.Width 1.3
## 505 55 Petal.Width 1.5
## 506 56 Petal.Width 1.3
## 507 57 Petal.Width 1.6
## 508 58 Petal.Width 1
## 509 59 Petal.Width 1.3
## 510 60 Petal.Width 1.4
## 511 61 Petal.Width 1
## 512 62 Petal.Width 1.5
## 513 63 Petal.Width 1
## 514 64 Petal.Width 1.4
## 515 65 Petal.Width 1.3
## 516 66 Petal.Width 1.4
## 517 67 Petal.Width 1.5
## 518 68 Petal.Width 1
## 519 69 Petal.Width 1.5
## 520 70 Petal.Width 1.1
## 521 71 Petal.Width 1.8
## 522 72 Petal.Width 1.3
## 523 73 Petal.Width 1.5
## 524 74 Petal.Width 1.2
## 525 75 Petal.Width 1.3
## 526 76 Petal.Width 1.4
## 527 77 Petal.Width 1.4
## 528 78 Petal.Width 1.7
## 529 79 Petal.Width 1.5
## 530 80 Petal.Width 1
## 531 81 Petal.Width 1.1
## 532 82 Petal.Width 1
## 533 83 Petal.Width 1.2
## 534 84 Petal.Width 1.6
## 535 85 Petal.Width 1.5
## 536 86 Petal.Width 1.6
## 537 87 Petal.Width 1.5
## 538 88 Petal.Width 1.3
## 539 89 Petal.Width 1.3
## 540 90 Petal.Width 1.3
## 541 91 Petal.Width 1.2
## 542 92 Petal.Width 1.4
## 543 93 Petal.Width 1.2
## 544 94 Petal.Width 1
## 545 95 Petal.Width 1.3
## 546 96 Petal.Width 1.2
## 547 97 Petal.Width 1.3
## 548 98 Petal.Width 1.3
## 549 99 Petal.Width 1.1
## 550 100 Petal.Width 1.3
## 551 101 Petal.Width 2.5
## 552 102 Petal.Width 1.9
## 553 103 Petal.Width 2.1
## 554 104 Petal.Width 1.8
## 555 105 Petal.Width 2.2
## 556 106 Petal.Width 2.1
## 557 107 Petal.Width 1.7
## 558 108 Petal.Width 1.8
## 559 109 Petal.Width 1.8
## 560 110 Petal.Width 2.5
## 561 111 Petal.Width 2
## 562 112 Petal.Width 1.9
## 563 113 Petal.Width 2.1
## 564 114 Petal.Width 2
## 565 115 Petal.Width 2.4
## 566 116 Petal.Width 2.3
## 567 117 Petal.Width 1.8
## 568 118 Petal.Width 2.2
## 569 119 Petal.Width 2.3
## 570 120 Petal.Width 1.5
## 571 121 Petal.Width 2.3
## 572 122 Petal.Width 2
## 573 123 Petal.Width 2
## 574 124 Petal.Width 1.8
## 575 125 Petal.Width 2.1
## 576 126 Petal.Width 1.8
## 577 127 Petal.Width 1.8
## 578 128 Petal.Width 1.8
## 579 129 Petal.Width 2.1
## 580 130 Petal.Width 1.6
## 581 131 Petal.Width 1.9
## 582 132 Petal.Width 2
## 583 133 Petal.Width 2.2
## 584 134 Petal.Width 1.5
## 585 135 Petal.Width 1.4
## 586 136 Petal.Width 2.3
## 587 137 Petal.Width 2.4
## 588 138 Petal.Width 1.8
## 589 139 Petal.Width 1.8
## 590 140 Petal.Width 2.1
## 591 141 Petal.Width 2.4
## 592 142 Petal.Width 2.3
## 593 143 Petal.Width 1.9
## 594 144 Petal.Width 2.3
## 595 145 Petal.Width 2.5
## 596 146 Petal.Width 2.3
## 597 147 Petal.Width 1.9
## 598 148 Petal.Width 2
## 599 149 Petal.Width 2.3
## 600 150 Petal.Width 1.8
## 601 1 Species setosa
## 602 2 Species setosa
## 603 3 Species setosa
## 604 4 Species setosa
## 605 5 Species setosa
## 606 6 Species setosa
## 607 7 Species setosa
## 608 8 Species setosa
## 609 9 Species setosa
## 610 10 Species setosa
## 611 11 Species setosa
## 612 12 Species setosa
## 613 13 Species setosa
## 614 14 Species setosa
## 615 15 Species setosa
## 616 16 Species setosa
## 617 17 Species setosa
## 618 18 Species setosa
## 619 19 Species setosa
## 620 20 Species setosa
## 621 21 Species setosa
## 622 22 Species setosa
## 623 23 Species setosa
## 624 24 Species setosa
## 625 25 Species setosa
## 626 26 Species setosa
## 627 27 Species setosa
## 628 28 Species setosa
## 629 29 Species setosa
## 630 30 Species setosa
## 631 31 Species setosa
## 632 32 Species setosa
## 633 33 Species setosa
## 634 34 Species setosa
## 635 35 Species setosa
## 636 36 Species setosa
## 637 37 Species setosa
## 638 38 Species setosa
## 639 39 Species setosa
## 640 40 Species setosa
## 641 41 Species setosa
## 642 42 Species setosa
## 643 43 Species setosa
## 644 44 Species setosa
## 645 45 Species setosa
## 646 46 Species setosa
## 647 47 Species setosa
## 648 48 Species setosa
## 649 49 Species setosa
## 650 50 Species setosa
## 651 51 Species versicolor
## 652 52 Species versicolor
## 653 53 Species versicolor
## 654 54 Species versicolor
## 655 55 Species versicolor
## 656 56 Species versicolor
## 657 57 Species versicolor
## 658 58 Species versicolor
## 659 59 Species versicolor
## 660 60 Species versicolor
## 661 61 Species versicolor
## 662 62 Species versicolor
## 663 63 Species versicolor
## 664 64 Species versicolor
## 665 65 Species versicolor
## 666 66 Species versicolor
## 667 67 Species versicolor
## 668 68 Species versicolor
## 669 69 Species versicolor
## 670 70 Species versicolor
## 671 71 Species versicolor
## 672 72 Species versicolor
## 673 73 Species versicolor
## 674 74 Species versicolor
## 675 75 Species versicolor
## 676 76 Species versicolor
## 677 77 Species versicolor
## 678 78 Species versicolor
## 679 79 Species versicolor
## 680 80 Species versicolor
## 681 81 Species versicolor
## 682 82 Species versicolor
## 683 83 Species versicolor
## 684 84 Species versicolor
## 685 85 Species versicolor
## 686 86 Species versicolor
## 687 87 Species versicolor
## 688 88 Species versicolor
## 689 89 Species versicolor
## 690 90 Species versicolor
## 691 91 Species versicolor
## 692 92 Species versicolor
## 693 93 Species versicolor
## 694 94 Species versicolor
## 695 95 Species versicolor
## 696 96 Species versicolor
## 697 97 Species versicolor
## 698 98 Species versicolor
## 699 99 Species versicolor
## 700 100 Species versicolor
## 701 101 Species virginica
## 702 102 Species virginica
## 703 103 Species virginica
## 704 104 Species virginica
## 705 105 Species virginica
## 706 106 Species virginica
## 707 107 Species virginica
## 708 108 Species virginica
## 709 109 Species virginica
## 710 110 Species virginica
## 711 111 Species virginica
## 712 112 Species virginica
## 713 113 Species virginica
## 714 114 Species virginica
## 715 115 Species virginica
## 716 116 Species virginica
## 717 117 Species virginica
## 718 118 Species virginica
## 719 119 Species virginica
## 720 120 Species virginica
## 721 121 Species virginica
## 722 122 Species virginica
## 723 123 Species virginica
## 724 124 Species virginica
## 725 125 Species virginica
## 726 126 Species virginica
## 727 127 Species virginica
## 728 128 Species virginica
## 729 129 Species virginica
## 730 130 Species virginica
## 731 131 Species virginica
## 732 132 Species virginica
## 733 133 Species virginica
## 734 134 Species virginica
## 735 135 Species virginica
## 736 136 Species virginica
## 737 137 Species virginica
## 738 138 Species virginica
## 739 139 Species virginica
## 740 140 Species virginica
## 741 141 Species virginica
## 742 142 Species virginica
## 743 143 Species virginica
## 744 144 Species virginica
## 745 145 Species virginica
## 746 146 Species virginica
## 747 147 Species virginica
## 748 148 Species virginica
## 749 149 Species virginica
## 750 150 Species virginicaQuindi ogni soggetto (identificato dal campo id, inserito apposta) avrà dati in più righe, e precisamente nel campo value, mentre la colonna variable specifica a quale variabile è riferito il valore di value. Il lettore attento noterà che siamo passati dal formato wide al formato long usando funzioni non sono nel pacchetto base di R ma del pacchetto reshape2, ma per ora sorvoleremo (e il lettore ci perdonerà) e torneremo su questo punto più avanti. Intanto ragioniamo sul fatto che il formato wide è più familiare (praticamente è una tabella) e semplice da compilare, ma il formato long è molto più efficiente e sicuro. Per comprendere il perchè di questa affermazione prendiamo il caso di un grande dataset che debba essere continuamente aggiornato, magari con osservazioni (nuove righe) non omogee rispetto alle precedenti (ad esempio abbiamo misurato una nuova biometria rispetto a quelle precedenti). Si può capire facilmente che sarebbe molto più facile aggiungere questa nuova osservazione al data frame long, poichè dovremmo specificare i valori solo per il nuovo record. Se invece dovessimo aggiungere la nuova osservazione al data frame wide, e ci trovassimo ad aver misurato una nuova biometria, sarebbe necessario modificare tutti i record precedenti aggiungendo un NA nella nuova colonna per la nuova biometria.
La funzione data.frame permette di generare questo genere di oggetti da qualsiasi tipo di dato. Leggendo il suo help, noteremo che alla voce usage compaiono tre puntini al posto degli argomenti, e per il resto ci sono solo opzioni.
4.14.8 vector
Dopo aver descritto le funzioni specifiche per generare vettori di varie classi, vediamo la funzione generica vector che serve a generare vettori di qualunque tipo. In effetti, vector ha come argomenti mode, cioè la classe del vettore da generare, e length che ha lo stesso significato visto per numeric e character.
4.14.9 rep
Anche questa funzione serve per generare vettori, ma questa volta usando la replicazione di elementi forniti dall’utente. rep vuole due argomenti, il primo dei quali (x) corrisponde gli elementi da replicare, mentre il secondo può essere times, cioè il numero di volte che x (in blocco) deve essere replicato, oppure length.out, cioè la lunghezza del vettore che si vuole ottenere. Vediamo degli esempi:
## [1] 1 1 1 1 1## [1] "a" "a" "a" "a" "a"## [1] 1 2 1 2 1 2Nel primo caso abbiamo replicato un numero, nel secondo una lettera, nel terzo un vettore
## [1] 1 1 1 1 1 1 1In questo caso, invece, abbiamo fissato la lunghezza del vettore.
4.14.10 seq
Questa funzione serve a generare sequenze regolari di valori numerici. I suoi argomenti sono from (cioè il punto di partenza della serie regolare - il suo minimo insomma), to (il suo massimo, che però può non coincidere con il punto finale della serie generata) e, a scelta, by (il passo della sequenza) o length.out (la lunghezza del vettore). Vediamo alcuni esempi:
## [1] 1 2 3 4 5 6 7 8 9 10## [1] 1 3 5 7 9## [1] 1.0 1.9 2.8 3.7 4.6 5.5 6.4 7.3 8.2 9.1 10.0Il primo esempio è molto semplice: generiamo una sequenza da 1 a 10 con passo 1. Il secondo, in cui partiamo da 1 e “puntiamo” a 10 ma con passo 2, R si ferma a 9 poichè aggiungere un altro passo significherebbe ottenere 11 e quindi superare il massimo fissato (10). Nel terzo esempio abbiamo ottenuto un vettore con estremi coincidenti con i valori di from e to ma con un intervallo decimale poichè abbiamo fissato il numero di elementi del vettore e, quindi, R ha calcolato il passo corrispondente per arrivare da 1 a 10 con 10 passi.
A questo punto, passiamo alle funzioni per esplorare gli oggetti.
4.14.11 head e tail
Queste due funzioni sono molto utili per avere una visione parziale di diversi oggetti, come per esempio i data frame. Nello specifico, head permette di visualizzare dal terminale la testa, cioè le prime righe del data frame, mentre tail permette di visualizzare la coda. Entrambi i comandi vogliono un argomento obbligato, x, cioè l’oggetto di cui si vuola visualizzare le prime o le ultime n righe, dove n è un argomento opzionale, fissato come valore di default a 6. Modificando questo parametro, si possono visualizzare le prime (o le ultime) 10, 20, 30 righe.
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species id
## 1 5.1 3.5 1.4 0.2 setosa 1
## 2 4.9 3.0 1.4 0.2 setosa 2
## 3 4.7 3.2 1.3 0.2 setosa 3
## 4 4.6 3.1 1.5 0.2 setosa 4
## 5 5.0 3.6 1.4 0.2 setosa 5
## 6 5.4 3.9 1.7 0.4 setosa 6## Sepal.Length Sepal.Width Petal.Length Petal.Width Species id
## 1 5.1 3.5 1.4 0.2 setosa 1
## 2 4.9 3.0 1.4 0.2 setosa 2
## 3 4.7 3.2 1.3 0.2 setosa 3
## 4 4.6 3.1 1.5 0.2 setosa 4
## 5 5.0 3.6 1.4 0.2 setosa 5
## 6 5.4 3.9 1.7 0.4 setosa 6
## 7 4.6 3.4 1.4 0.3 setosa 7
## 8 5.0 3.4 1.5 0.2 setosa 8
## 9 4.4 2.9 1.4 0.2 setosa 9
## 10 4.9 3.1 1.5 0.1 setosa 10## Sepal.Length Sepal.Width Petal.Length Petal.Width Species id
## 145 6.7 3.3 5.7 2.5 virginica 145
## 146 6.7 3.0 5.2 2.3 virginica 146
## 147 6.3 2.5 5.0 1.9 virginica 147
## 148 6.5 3.0 5.2 2.0 virginica 148
## 149 6.2 3.4 5.4 2.3 virginica 149
## 150 5.9 3.0 5.1 1.8 virginica 150## Sepal.Length Sepal.Width Petal.Length Petal.Width Species id
## 141 6.7 3.1 5.6 2.4 virginica 141
## 142 6.9 3.1 5.1 2.3 virginica 142
## 143 5.8 2.7 5.1 1.9 virginica 143
## 144 6.8 3.2 5.9 2.3 virginica 144
## 145 6.7 3.3 5.7 2.5 virginica 145
## 146 6.7 3.0 5.2 2.3 virginica 146
## 147 6.3 2.5 5.0 1.9 virginica 147
## 148 6.5 3.0 5.2 2.0 virginica 148
## 149 6.2 3.4 5.4 2.3 virginica 149
## 150 5.9 3.0 5.1 1.8 virginica 1504.14.12 nrow, ncol, dim e length
Facciamo finta di essere alle prese con un data frame che non conosciamo. Probabilmente una delle prime cose da fare è indagare la geometria del data frame, cioè capire quante righe e quante osservazioni ci sono. La funzione nrow ci fornisce il numero di righe, ncol ci fornisce il numero di colonne. dim e li fornisce entrambi. Nel caso degli array, dim ci restituisce tutte le dimensioni dell’ array stesso.
## [1] 150## [1] 6## [1] 150 6## [1] 3 3 2length ci fornisce il numero di elementi che caratterizzano un vettore, ma si applica a qualsiasi oggetto di R, che come sappiamo è sempre visto da R come una struttura vettoriale.
## [1] 150## [1] 64.14.13 str
A parte le dimensioni, è importante conoscere la struttura dei dati, cioè le classi delle colonne del data frame (o di qualsiasi altro oggetto). Vediamo un esempio:
## 'data.frame': 150 obs. of 6 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ id : int 1 2 3 4 5 6 7 8 9 10 ...Come possiamo vedere, R ci dice le dimensioni ma, ma anche la classe di ogni singola colonna/variabile.
## int [1:3, 1:3] 1 2 3 4 5 6 7 8 94.14.14 class
Questa funzione, che abbiamo già incontrato, ci dice a quale classe specifica appartiene un dato oggetto.
## [1] "numeric"## [1] "factor"## [1] "data.frame"4.14.15 unique
Questa funzione ci permette di estrarre i valori univoci di qualsiasi oggetto, cioè tutti i valori che ricorrono almeno una volta. Vediamo degli esempi:
## [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.4 4.8 4.3 5.8 5.7 5.2 5.5 4.5 5.3 7.0 6.4 6.9 6.5
## [20] 6.3 6.6 5.9 6.0 6.1 5.6 6.7 6.2 6.8 7.1 7.6 7.3 7.2 7.7 7.4 7.9## [1] setosa versicolor virginica
## Levels: setosa versicolor virginica## Sepal.Length Sepal.Width Petal.Length Petal.Width Species id
## 1 5.1 3.5 1.4 0.2 setosa 1
## 2 4.9 3.0 1.4 0.2 setosa 2
## 3 4.7 3.2 1.3 0.2 setosa 3
## 4 4.6 3.1 1.5 0.2 setosa 4
## 5 5.0 3.6 1.4 0.2 setosa 5
## 6 5.4 3.9 1.7 0.4 setosa 6
## 7 4.6 3.4 1.4 0.3 setosa 7
## 8 5.0 3.4 1.5 0.2 setosa 8
## 9 4.4 2.9 1.4 0.2 setosa 9
## 10 4.9 3.1 1.5 0.1 setosa 10
## 11 5.4 3.7 1.5 0.2 setosa 11
## 12 4.8 3.4 1.6 0.2 setosa 12
## 13 4.8 3.0 1.4 0.1 setosa 13
## 14 4.3 3.0 1.1 0.1 setosa 14
## 15 5.8 4.0 1.2 0.2 setosa 15
## 16 5.7 4.4 1.5 0.4 setosa 16
## 17 5.4 3.9 1.3 0.4 setosa 17
## 18 5.1 3.5 1.4 0.3 setosa 18
## 19 5.7 3.8 1.7 0.3 setosa 19
## 20 5.1 3.8 1.5 0.3 setosa 20
## 21 5.4 3.4 1.7 0.2 setosa 21
## 22 5.1 3.7 1.5 0.4 setosa 22
## 23 4.6 3.6 1.0 0.2 setosa 23
## 24 5.1 3.3 1.7 0.5 setosa 24
## 25 4.8 3.4 1.9 0.2 setosa 25
## 26 5.0 3.0 1.6 0.2 setosa 26
## 27 5.0 3.4 1.6 0.4 setosa 27
## 28 5.2 3.5 1.5 0.2 setosa 28
## 29 5.2 3.4 1.4 0.2 setosa 29
## 30 4.7 3.2 1.6 0.2 setosa 30
## 31 4.8 3.1 1.6 0.2 setosa 31
## 32 5.4 3.4 1.5 0.4 setosa 32
## 33 5.2 4.1 1.5 0.1 setosa 33
## 34 5.5 4.2 1.4 0.2 setosa 34
## 35 4.9 3.1 1.5 0.2 setosa 35
## 36 5.0 3.2 1.2 0.2 setosa 36
## 37 5.5 3.5 1.3 0.2 setosa 37
## 38 4.9 3.6 1.4 0.1 setosa 38
## 39 4.4 3.0 1.3 0.2 setosa 39
## 40 5.1 3.4 1.5 0.2 setosa 40
## 41 5.0 3.5 1.3 0.3 setosa 41
## 42 4.5 2.3 1.3 0.3 setosa 42
## 43 4.4 3.2 1.3 0.2 setosa 43
## 44 5.0 3.5 1.6 0.6 setosa 44
## 45 5.1 3.8 1.9 0.4 setosa 45
## 46 4.8 3.0 1.4 0.3 setosa 46
## 47 5.1 3.8 1.6 0.2 setosa 47
## 48 4.6 3.2 1.4 0.2 setosa 48
## 49 5.3 3.7 1.5 0.2 setosa 49
## 50 5.0 3.3 1.4 0.2 setosa 50
## 51 7.0 3.2 4.7 1.4 versicolor 51
## 52 6.4 3.2 4.5 1.5 versicolor 52
## 53 6.9 3.1 4.9 1.5 versicolor 53
## 54 5.5 2.3 4.0 1.3 versicolor 54
## 55 6.5 2.8 4.6 1.5 versicolor 55
## 56 5.7 2.8 4.5 1.3 versicolor 56
## 57 6.3 3.3 4.7 1.6 versicolor 57
## 58 4.9 2.4 3.3 1.0 versicolor 58
## 59 6.6 2.9 4.6 1.3 versicolor 59
## 60 5.2 2.7 3.9 1.4 versicolor 60
## 61 5.0 2.0 3.5 1.0 versicolor 61
## 62 5.9 3.0 4.2 1.5 versicolor 62
## 63 6.0 2.2 4.0 1.0 versicolor 63
## 64 6.1 2.9 4.7 1.4 versicolor 64
## 65 5.6 2.9 3.6 1.3 versicolor 65
## 66 6.7 3.1 4.4 1.4 versicolor 66
## 67 5.6 3.0 4.5 1.5 versicolor 67
## 68 5.8 2.7 4.1 1.0 versicolor 68
## 69 6.2 2.2 4.5 1.5 versicolor 69
## 70 5.6 2.5 3.9 1.1 versicolor 70
## 71 5.9 3.2 4.8 1.8 versicolor 71
## 72 6.1 2.8 4.0 1.3 versicolor 72
## 73 6.3 2.5 4.9 1.5 versicolor 73
## 74 6.1 2.8 4.7 1.2 versicolor 74
## 75 6.4 2.9 4.3 1.3 versicolor 75
## 76 6.6 3.0 4.4 1.4 versicolor 76
## 77 6.8 2.8 4.8 1.4 versicolor 77
## 78 6.7 3.0 5.0 1.7 versicolor 78
## 79 6.0 2.9 4.5 1.5 versicolor 79
## 80 5.7 2.6 3.5 1.0 versicolor 80
## 81 5.5 2.4 3.8 1.1 versicolor 81
## 82 5.5 2.4 3.7 1.0 versicolor 82
## 83 5.8 2.7 3.9 1.2 versicolor 83
## 84 6.0 2.7 5.1 1.6 versicolor 84
## 85 5.4 3.0 4.5 1.5 versicolor 85
## 86 6.0 3.4 4.5 1.6 versicolor 86
## 87 6.7 3.1 4.7 1.5 versicolor 87
## 88 6.3 2.3 4.4 1.3 versicolor 88
## 89 5.6 3.0 4.1 1.3 versicolor 89
## 90 5.5 2.5 4.0 1.3 versicolor 90
## 91 5.5 2.6 4.4 1.2 versicolor 91
## 92 6.1 3.0 4.6 1.4 versicolor 92
## 93 5.8 2.6 4.0 1.2 versicolor 93
## 94 5.0 2.3 3.3 1.0 versicolor 94
## 95 5.6 2.7 4.2 1.3 versicolor 95
## 96 5.7 3.0 4.2 1.2 versicolor 96
## 97 5.7 2.9 4.2 1.3 versicolor 97
## 98 6.2 2.9 4.3 1.3 versicolor 98
## 99 5.1 2.5 3.0 1.1 versicolor 99
## 100 5.7 2.8 4.1 1.3 versicolor 100
## 101 6.3 3.3 6.0 2.5 virginica 101
## 102 5.8 2.7 5.1 1.9 virginica 102
## 103 7.1 3.0 5.9 2.1 virginica 103
## 104 6.3 2.9 5.6 1.8 virginica 104
## 105 6.5 3.0 5.8 2.2 virginica 105
## 106 7.6 3.0 6.6 2.1 virginica 106
## 107 4.9 2.5 4.5 1.7 virginica 107
## 108 7.3 2.9 6.3 1.8 virginica 108
## 109 6.7 2.5 5.8 1.8 virginica 109
## 110 7.2 3.6 6.1 2.5 virginica 110
## 111 6.5 3.2 5.1 2.0 virginica 111
## 112 6.4 2.7 5.3 1.9 virginica 112
## 113 6.8 3.0 5.5 2.1 virginica 113
## 114 5.7 2.5 5.0 2.0 virginica 114
## 115 5.8 2.8 5.1 2.4 virginica 115
## 116 6.4 3.2 5.3 2.3 virginica 116
## 117 6.5 3.0 5.5 1.8 virginica 117
## 118 7.7 3.8 6.7 2.2 virginica 118
## 119 7.7 2.6 6.9 2.3 virginica 119
## 120 6.0 2.2 5.0 1.5 virginica 120
## 121 6.9 3.2 5.7 2.3 virginica 121
## 122 5.6 2.8 4.9 2.0 virginica 122
## 123 7.7 2.8 6.7 2.0 virginica 123
## 124 6.3 2.7 4.9 1.8 virginica 124
## 125 6.7 3.3 5.7 2.1 virginica 125
## 126 7.2 3.2 6.0 1.8 virginica 126
## 127 6.2 2.8 4.8 1.8 virginica 127
## 128 6.1 3.0 4.9 1.8 virginica 128
## 129 6.4 2.8 5.6 2.1 virginica 129
## 130 7.2 3.0 5.8 1.6 virginica 130
## 131 7.4 2.8 6.1 1.9 virginica 131
## 132 7.9 3.8 6.4 2.0 virginica 132
## 133 6.4 2.8 5.6 2.2 virginica 133
## 134 6.3 2.8 5.1 1.5 virginica 134
## 135 6.1 2.6 5.6 1.4 virginica 135
## 136 7.7 3.0 6.1 2.3 virginica 136
## 137 6.3 3.4 5.6 2.4 virginica 137
## 138 6.4 3.1 5.5 1.8 virginica 138
## 139 6.0 3.0 4.8 1.8 virginica 139
## 140 6.9 3.1 5.4 2.1 virginica 140
## 141 6.7 3.1 5.6 2.4 virginica 141
## 142 6.9 3.1 5.1 2.3 virginica 142
## 143 5.8 2.7 5.1 1.9 virginica 143
## 144 6.8 3.2 5.9 2.3 virginica 144
## 145 6.7 3.3 5.7 2.5 virginica 145
## 146 6.7 3.0 5.2 2.3 virginica 146
## 147 6.3 2.5 5.0 1.9 virginica 147
## 148 6.5 3.0 5.2 2.0 virginica 148
## 149 6.2 3.4 5.4 2.3 virginica 149
## 150 5.9 3.0 5.1 1.8 virginica 150Nell’ultimo esempio abbiamo usato la funzione unique sull’intero data frame. R non ha fatto altro che interpretare le righe (cioè le osservazioni) come unità costitutive del data frame e quindi ha restituito un oggetto con struttura analoga al data frame di partenza ma aventi un numero di righe inferiore se ci fossero individui (righe) perfettamente uguali, cosa che per iris non succede. Ma proviamo a truccare i dati e usiamo dim per vedere cosa succede.
## [1] 150 6## [1] 150 6## [1] 149 6Abbiamo sovrascritto la seconda riga di iris ponendola uguale alla quinta, e infatti adesso il numero di righe univoche è 149.
4.14.16 table
Continuando ad approfondire, potremmo volevo capire quale è il numero di osservazioni per ciascuna combinazione di variabili. Nel caso di iris, abbiamo visto come usare unique per capire, ad esempio, quali specie del genere iris sono contenute nel data frame.
## [1] setosa versicolor virginica
## Levels: setosa versicolor virginicaAdesso, vediamo come table ci fornisce il numero di occorrenze per ogni specie.
##
## setosa versicolor virginica
## 50 50 50Gli oggetti che restituisce questa funzione sono delle tabelle che corrispondono a vettori nel caso in cui siano stati generati da un vettore (una singola variabile).
Quella dell’esempio è una tabella di contingenza per la variabile specie, ma possiamo ottenere tabella combinando più variabili, dandole come argomento a table e separandolo, come sempre, con le virgole. Vediamo un esempio intuitivo.
iris$color = factor(rep(c("red","blue"), 75),
levels = c("red","blue"))
table(iris$color, iris$Species)##
## setosa versicolor virginica
## red 25 25 25
## blue 25 25 25In questo caso abbiamo generato una nuova colonna di iris, chiamata color, e contenente valori casuali di rosso e di blu.
4.14.17 rev, sort e order
rev è una funzione di semplicissimo utilizzo ci permette di rovesciare dei vettori. Ad esempio:
## [1] 10 9 8 7 6 5 4 3 2 1sort ci permette, invece, di ordinare un vettore rispetto ai valori dei suoi elementi. Ha un’opzione, decreasing, che ci consente di scegliere tra ordine crescente, impostato come default, e decrescente.
## [1] 1 5 23 42 43 46 67 68 75 97## [1] 97 75 68 67 46 43 42 23 5 1order, infine, ci permette di estrarre gli indici di posizione ordinati degli elementi di un oggetto.
## [1] 87 33 7 13 40 35 12 96 80 16## [1] 7 12 13 16 33 35 40 80 87 96## [1] 3 7 4 10 2 6 5 9 1 8## [1] 8 1 9 5 6 2 10 4 7 3Passiamo ora a un gruppo di funzione utili per combinare tra loro diversi oggetti.
4.14.18 sample
Più che per la combinazione, sample serve per la ri-combinazione: mediante questa funzione è possibile generare un nuovo vettore campionando (sampling) gli elementi di un altro vettore. Gli argomenti da fornire a questa funzione sono:
- x, cioè l’insieme dei dati da cui estrarre i valori campionati. Generalmente è un vettore numerico ma può essere anche di altro tipo
- size, cioè il numero di osservazioni che vogliamo estrarre. Qui può nascere un problema. Di default, sample si comporta come il croupier nella tombola: ogni elemento estratto da x viene rimosso da x, per cui x non può contenere un numero di elementi minore del valore di size…. a meno che….
- replace (o rep) è l’opzione che, se impostata come TRUE, autorizza R a ricampionare gli stessi elementi di x, senza rimuovere i valori estratti
- Sempre per default, la funzione sample estrae “a caso”gli elementi di x assegnando a ciascuno di essi la stessa probabilità di estrazione. Mediante l’argomento prob è possibile però indicare a R un valori di probabilità per ogni elemento di x.
Esaminiamo alcuni esempi:
## [1] 8 7 5## [1] 8 7 10 2 6 1 8 4 2 1 1 6 5 8 7 3 6 10 7 1## [1] 7 1 1 1 1 1 1 1 1 3 1 10 4 3 1 10 5 1 4 6 1 4 1 10 4
## [26] 1 8 4 1 1Dunque, nei primi due esempi abbiamo visto come usare l’opzione rep, nell’ultimo esempio possiamo notare come le probabilità di estrazione, fortemente sbilanciate a favore del valore 1, si riflettono sulla composizione del campione estratto.
4.14.19 cbind e rbind
Queste due funzioni ci consentono di “incollare” insieme vettori, matrici o data frame. In particolare cbind (column bind) permette di incollare colonne, mentre rbind permette di incollare righe. Il vincolo principale di queste operazioni è legato alla coerenza della geometria, degli attributi e anche dei nomi. Ad esempio, posso incollare insieme righe di due data frame se esse sono omogenee rispetto alle colonne
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 51 7.0 3.2 4.7 1.4 versicolor
## 150 5.9 3.0 5.1 1.8 virginica4.14.20 which
Abbiamo già parlato di questa funzione in precedenza (Sezione 4.12 a proposito dell’Algebra di Boole).
4.14.21 match
Si tratta di una funzione molto utile per associare vettori diversi. Nello specifico, match individua tutti gli elementi del vettore x (primo argomento) che corrispondono a elementi del vettore table (secondo argomento). Vediamo due esempi
## [1] 1 2 2 3 1## [1] 1 2 4 NA NA NA NAAbbiamo generato due vettori, v1 e v2, il primo dei quali contiene meno valori univoci e alcune duplicazioni rispetto al secondo. Quando abbiamo confrontato il primo vettore usando come riferimento (table) il secondo, otteniamo dei valori numerici che altro non sono se non gli indici di posizione degli elementi di v1 rispetto a v2. Viceversa, abbiamo ottenuto 3 valori numerici e 4 NA poichè gli ultimi 4 elementi di v2 non hanno riscontro in v1.
4.14.22 intersect, setdiff, e union
Con questa triade di funzioni facciamo capolino nel salotto di George Boole. Come suggeriscono i loro nomi, intersect serve a fare intersezioni, union a fare unioni e setdiff calcolare la differenza simmetrica (insieme complementare). Ad esempio:
## [1] "A" "B" "C"## [1] "A" "B" "C" "H" "D" "E" "F" "G"## [1] "H"## [1] "D" "E" "F" "G"I primi due esempi sono immediati. Gli altri due meritano di essere guardati meglio: a seconda dell’ordine con cui forniamo gli argomenti otteniamo delle differenze simmetriche diverse. In particolare, otteniamo gli elementi del primo insieme che non sono comuni al secondo. Il limite di queste funzioni è che sono tutte capaci di operare solo su 2 argomenti alla volta.
4.14.23 merge
Chiunque abbiamo “risistemato” dei dati con un foglio di calcolo tipo excel sa bene come va a finire quando dobbiamo appaiare degli insiemi di dati che “si parlano” tra loro mediante una o più colonne ma differiscono per altre. Un gran pasticcio, che diventa ingestibile quando i dataset sono grandi e articolati. La funzione merge serve proprio per fondere due data frame che abbiano in comune delle colonne (usate come riferimento). Ad esempio:
data(iris)
iris$id = 1:150
iris_c = data.frame(id = sample(1:150,150),
color = factor(rep(c("red","blue"), 75),
levels = c("red","blue")))
head(iris_c)## id color
## 1 127 red
## 2 71 blue
## 3 88 red
## 4 20 blue
## 5 63 red
## 6 45 blue## id Sepal.Length Sepal.Width Petal.Length Petal.Width Species color
## 1 1 5.1 3.5 1.4 0.2 setosa blue
## 2 2 4.9 3.0 1.4 0.2 setosa blue
## 3 3 4.7 3.2 1.3 0.2 setosa red
## 4 4 4.6 3.1 1.5 0.2 setosa red
## 5 5 5.0 3.6 1.4 0.2 setosa red
## 6 6 5.4 3.9 1.7 0.4 setosa red
## 7 7 4.6 3.4 1.4 0.3 setosa blue
## 8 8 5.0 3.4 1.5 0.2 setosa blue
## 9 9 4.4 2.9 1.4 0.2 setosa blue
## 10 10 4.9 3.1 1.5 0.1 setosa red
## 11 11 5.4 3.7 1.5 0.2 setosa blue
## 12 12 4.8 3.4 1.6 0.2 setosa red
## 13 13 4.8 3.0 1.4 0.1 setosa red
## 14 14 4.3 3.0 1.1 0.1 setosa blue
## 15 15 5.8 4.0 1.2 0.2 setosa blue
## 16 16 5.7 4.4 1.5 0.4 setosa blue
## 17 17 5.4 3.9 1.3 0.4 setosa blue
## 18 18 5.1 3.5 1.4 0.3 setosa red
## 19 19 5.7 3.8 1.7 0.3 setosa blue
## 20 20 5.1 3.8 1.5 0.3 setosa blueNoterete che:
- abbiamo aggiunto a iris il campo id come un progressivo numerico da 1 a 150
- abbiamo creato un data frame (iris_c) contente un campo id analogo a quello di iris, ma con valori casuali (usando opportunamento la funzione sample)
- quindi abbiamo accoppiato i due data frame iris e iris_c usando merge. Merge è capace di lavorare in autonomia individuando le colonne in comune tra i due data frame e, se queste sono omogenee (la variabile id non può essere numerica in un caso e character in un altro), le usa per fondere i due data frame. Tuttavia questa funzione possiede alcuni argomenti opzionali (by, by.x, by.y) che ci consentono di specificare quali colonne usare o quali righe usare.
4.14.24 apply
Abbiamo già avuto modo di spiegare che i data frame non sono oggetti ottimizzati per fare i calcoli. Sono utilissimi per gestire i dati, ma non possiamo applicare ad essi funzioni estramemente utili come apply. Per capire a cosa serve questa funzione prendiamo un esempio: abbiamo bisogno di calcolare (per motivi oscuri) il valore medio delle 4 biometrie contenute in iris. Come possiamo fare? E’ evidente che calcolare riga per riga le medie è un’operazione laboriosa… a parte il fatto che dovremo limitare il calcolo alle prime 4 colonne del data frame.
data(iris)
b1 = mean(as.numeric(iris[,1]))
b2 = mean(as.numeric(iris[,2]))
b3 = mean(as.numeric(iris[,3]))
b4 = mean(as.numeric(iris[,4]))
b1## [1] 5.843333## [1] 3.057333## [1] 3.758## [1] 1.199333Ok, prima cosa: abbiamo introdotto di soppiatto la funzione mean, della quale parleremo tra poco. Per ora basti sapere che questa funzione consente di calcolare la media degli elementi di un vettore numerico. Torniamo alla domanda originale (calcolare il valore medio delle 4 biometrie contenute in iris, possibilmente in un’unica operazione)….. forse potremmo usare un ciclo iterativo?… ma non abbiamo ancora incontrato i cicli e spesso non sono il modo più veloce per fare operazioni di questo tipo.
apply ci viene in aiuto. Questa funzione ha 3 argomenti:
- X, cioè l’oggetto su cui applicare la funzione FUN. X può essere un qualsiasi oggetto assimilabile a un array numerico (se FUN si applica ai numeri) o non numerico (se FUN si applica anche ad altre classi)
- MARGIN, ovvero la “direzione” rispetto alla quale applicare FUN
- FUN, cioè la funzione che ci interessa applicare
Vediamo degli esempi
## [1] 2.550 2.375 2.350 2.350 2.550 2.850 2.425 2.525 2.225 2.400 2.700 2.500
## [13] 2.325 2.125 2.800 3.000 2.750 2.575 2.875 2.675 2.675 2.675 2.350 2.650
## [25] 2.575 2.450 2.600 2.600 2.550 2.425 2.425 2.675 2.725 2.825 2.425 2.400
## [37] 2.625 2.500 2.225 2.550 2.525 2.100 2.275 2.675 2.800 2.375 2.675 2.350
## [49] 2.675 2.475 4.075 3.900 4.100 3.275 3.850 3.575 3.975 2.900 3.850 3.300
## [61] 2.875 3.650 3.300 3.775 3.350 3.900 3.650 3.400 3.600 3.275 3.925 3.550
## [73] 3.800 3.700 3.725 3.850 3.950 4.100 3.725 3.200 3.200 3.150 3.400 3.850
## [85] 3.600 3.875 4.000 3.575 3.500 3.325 3.425 3.775 3.400 2.900 3.450 3.525
## [97] 3.525 3.675 2.925 3.475 4.525 3.875 4.525 4.150 4.375 4.825 3.400 4.575
## [109] 4.200 4.850 4.200 4.075 4.350 3.800 4.025 4.300 4.200 5.100 4.875 3.675
## [121] 4.525 3.825 4.800 3.925 4.450 4.550 3.900 3.950 4.225 4.400 4.550 5.025
## [133] 4.250 3.925 3.925 4.775 4.425 4.200 3.900 4.375 4.450 4.350 3.875 4.550
## [145] 4.550 4.300 3.925 4.175 4.325 3.950## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 5.843333 3.057333 3.758000 1.199333Nel primo esempio abbiamo applicato la funzione mean alle prime 4 colonne di iris (quelle con le biometrie), assegnando a MARGIN il valore 1 che, come spiega l’help di questa funzione, indica le righe. Di conseguenza, apply ci restituisce un vettore di 150 elementi (ovvero le righe di iris), ognuno corrispondente alle medie che, prima, ci eravano messi a calcolare una per una.
Nel secondo esempio abbiamo applicato la funzione mean alle prime 4 colonne di iris (quelle con le biometrie), assegnando a MARGIN il valore 2 che indica le colonne. Questa volta apply ci restituisce un vettore di soli 4 elementi (corrispondenti le colonne di iris). Vediamo un ultimo esempio che coinvolge la funzione length che già conosciamo
## [1] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
## [38] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
## [75] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
## [112] 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
## [149] 5 5## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 150 150 150 150 150Questa volta non è stato necessario restingere il valore di X alle prime 4 colonne.
Il prossimo gruppo da esaminare è quello delle funzioni statistiche di base. Cominciamo col dire che tutte queste funzioni si appliano a dati quantitativi e quindi essenzialmete della classe numeric.
4.14.25 min, max, range
Queste tre funzioni generiche calcolano il minimo (min), il massimo (max) e l’intervallo (range) di un insieme di dati. Vediamo alcuni esempi intuitivi.
## [1] 4.3## [1] 7.9## [1] 4.3 7.9In tutti questi casi abbiamo usato queste funzioni su vettori, vediamo cosa succede quando siamo alle prese con matrici o data frame.
## [1] 4 99## [1] 7.9Come di può vedere queste funzioni “mangiano” di tutto. In più sono in grado di ignorare i valori “strani” (i NA e i NaN). Per farlo, è necessario usare l’opzione na.rm.
## [1] NA NA## [1] 4 984.14.26 summary
Questa funzione è, se possibile, altrettanto generica di plot e, come suggerisce il suo nome, serve a ottenere una visione compatta ma completa delle caratteristiche di un insieme di dati. Vediamo come si comporta su vari oggetti.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 22.00 48.50 63.50 65.20 83.75 96.00## V1 V2 V3 V4 V5
## Min. :14.0 Min. :45.0 Min. :24 Min. :27.0 Min. :19.0
## 1st Qu.:28.0 1st Qu.:58.0 1st Qu.:34 1st Qu.:30.0 1st Qu.:39.0
## Median :33.0 Median :69.0 Median :71 Median :41.0 Median :61.0
## Mean :36.4 Mean :69.8 Mean :60 Mean :52.8 Mean :58.2
## 3rd Qu.:53.0 3rd Qu.:81.0 3rd Qu.:79 3rd Qu.:82.0 3rd Qu.:75.0
## Max. :54.0 Max. :96.0 Max. :92 Max. :84.0 Max. :97.0## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
## Species
## setosa :50
## versicolor:50
## virginica :50
##
##
## Nel primo caso, relativo al vettore vec, R ci ha restituito la suguente serie di valori:
- Min. il valore minimo
- 1st Qu. il primo quartile della distribuzione dei dati
- Median la mediana o secondo quartile
- Mean il valore medio
- 3rd Qu. il terzo quartile della distribuzione dei dati
- Max. il valore massimo
Nel caso della matrice m o del data frame iris, R ha restituito gli stesso valori ma per ogni colonna. Nel caso della colonna Species di iris, che è un factor, ci ha fornito il numero delle occorrenze per ciascuna valore.
La funzione summary, comunque, è molto utile anche per capire alla svelta se nell’oggetto che ci interessa ci solo valori mancanti. Ad esempio:
## Warning in log(sample(-100:100, 25)): Si è prodotto un NaN## [,1] [,2] [,3] [,4] [,5]
## [1,] 2.995732 NaN 3.044522 NaN NaN
## [2,] NaN 3.135494 1.791759 4.174387 4.532599
## [3,] NaN 3.583519 NaN 3.637586 NaN
## [4,] 3.526361 NaN 1.386294 4.043051 NaN
## [5,] NaN 2.639057 2.484907 NaN NaN## V1 V2 V3 V4
## Min. :2.996 Min. :2.639 Min. :1.386 Min. :3.638
## 1st Qu.:3.128 1st Qu.:2.887 1st Qu.:1.690 1st Qu.:3.840
## Median :3.261 Median :3.135 Median :2.138 Median :4.043
## Mean :3.261 Mean :3.119 Mean :2.177 Mean :3.952
## 3rd Qu.:3.394 3rd Qu.:3.360 3rd Qu.:2.625 3rd Qu.:4.109
## Max. :3.526 Max. :3.584 Max. :3.045 Max. :4.174
## NA's :3 NA's :2 NA's :1 NA's :2
## V5
## Min. :4.533
## 1st Qu.:4.533
## Median :4.533
## Mean :4.533
## 3rd Qu.:4.533
## Max. :4.533
## NA's :4Come si può vedere, in questo caso R ci fornisce anche il numero di NA (o di NaN, in questo caso non c’è differenza) per ciascuna colonna della matrice. Per generare i NaN abbiamo usato sample per estrarre 25 valori da un insieme che comprende numeri negativi e poi abbiamo usato la funzione log (logaritmo), che non è definita per i numeri negativi, per ottenere una matrice con una serie di NaN disposti a caso.
4.14.27 cumsum
Questa semplice funzione ci permette di calcolare la somma cumulata dei valori di un vettore.
## [1] 27 19 81 11 70 59 68 17 30 89## [1] 27 46 127 138 208 267 335 352 382 471Da notare che questa funzione non ha un opzione na.rm per cui un singolo NA o NaN nei dati di partenza può causare una “reazione a catena”.
4.14.28 median e mean
Queste due funzioni molto simili ci permettono di calcolare media e mediana, i principali indici di centralità, su un qualsiasi insieme di dati Entrambe la funzioni hanno l’opzione na.rm che chiedere a R di ignorare i valori anomali.
## Warning in log(sample(-100:100, 25)): Si è prodotto un NaN## [,1] [,2] [,3] [,4] [,5]
## [1,] 4.564348 2.079442 NaN NaN 4.094345
## [2,] NaN 3.931826 1.609438 3.912023 3.583519
## [3,] 2.833213 3.737670 NaN NaN 3.951244
## [4,] 4.442651 2.302585 3.688879 4.127134 3.663562
## [5,] NaN NaN NaN 4.262680 NaN## [1] NA## [1] NaN## [1] 3.824846## [1] 3.549035## Warning in mean.default(iris): l'argomento non è numerico o logico: restituisco
## NA## [1] NA## Warning in mean.default(iris[, 1:4]): l'argomento non è numerico o logico:
## restituisco NA## [1] NANegli ultimi due esempi abbiamo avuto problemi nell’applicare la funzione mean a iris, anche quando ci siamo limitati alle prime 4 colonne che sappiamo essere numeric. Questo accade spesso quando si usano funzioni “matematiche” ai data frame, e fin dal primo incontro con questi oggetti avevamo precisato che non sono ottimali per il calcolo. Qui aggiungeremo che, se proprio volessi calcolare la media delle prime 4 colonne di iris, sarò costretto a trattarle come una matrice.
## [1] 3.46454.14.29 weighted.mean
La funzione di R per il calcolo della media pesata. Ha bisogno di due input: la x, cioè il vettore dei valori per calcolare la media, e w, il vettore dei loro pesi. Se la somma di w è diversa da 1, i pesi sono standardizzati nell’intervallo 0-1 in modo che la loro somma sia 1.
## [1] 49.51364## [1] 49.513644.14.30 quantile
Abbiamo visto che summary ci fornisce i quartili. Nella statistica descrittiva, i quartili sono quei valori/modalità che ripartiscono la popolazione in quattro parti di uguale numerosità. I quartili sono un gruppo particolare di quantili. Il quantile di ordine α o α-quantili (con α un numero reale nell’intervallo [0,1]) è un valore qα che divide la popolazione in due parti, proporzionali ad α e (1-α) e caratterizzate da valori rispettivamente minori e maggiori di qα. Per poter calcolare un quantile di ordine α è necessario che il carattere sia almeno ordinato, cioè sia possibile definire un ordinamento sulle modalità.
La funzione quantile di R serve per calcolare i quantili di ordine α per un qualsiasi vettore numerico o di classi ordinali. I suoi argomenti sono x, il vettore, e probs, cioè le probabilità (α).
## 0% 33% 66% 99%
## 6.00 40.89 71.24 96.62In questo esempio, abbiamo diviso i dati in 3 blocchi omogenei. Ovviamente è possibile fare anche “tagli” più eterogenei.
## 0% 50% 70% 90%
## 5.0 43.5 64.6 77.44.14.31 sd
Un’altra funzione statistica di base, che serve a calcolare la standard deviation (deviazione standard) di una serie di dati. Si applica esattamente come mean o median, e come loro ha un’opzione na.rm.
## [1] 27.412784.14.32 runif e rnorm
R è prima di tutto un ambiente per la statistica applicata. In questo ambito la possibilità di estrarre valori da una distribuzione nota è molto utile. runif e rnorm sono solo due tra le tante funzione che iniziano per r e continuano con il nome della distribuzione da cui estrarre valori. Insieme a queste funzioni, e per tutte le principali distribuzioni di dati, ci sono poi d (calcolo della densità), p (calcolo della funzione di ripartizione), q (calcolo della funzione quantilica). Per brevità esamineremo solo le funzioni normale e uniforme, ma ci sono anche la gamma, la beta, la weibull, ecc.
Gli argomenti necessari per rnorm sono:
- n, il numero di elementi da estrarre
- mean, il valore medio della normale
- sd, la deviazione standard della normale
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -2.5854 -0.5367 0.1151 0.1264 0.7474 2.7001Gli argomenti necessari per runif sono:
- n, il numero di elementi da estrarre
- min, il valore minimo
- max, il valore massimo
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.99990 -0.61469 -0.05546 -0.05627 0.37841 0.95604Permettiamoci una piccolissima anticipazione (incontreremo la funzione per gli istrogrammi tra pochissimo) e usiamo un grafico per confrontare i risultati
vnorm = rnorm(n = 100, mean = 0, sd = 1)
vunif = runif(n = 100, min = -1, max = 1)
par(mfrow = c(1,2))
hist(vnorm, col = "grey", main = "dist normale")
hist(vunif, col = "grey", main = "dist uniforme")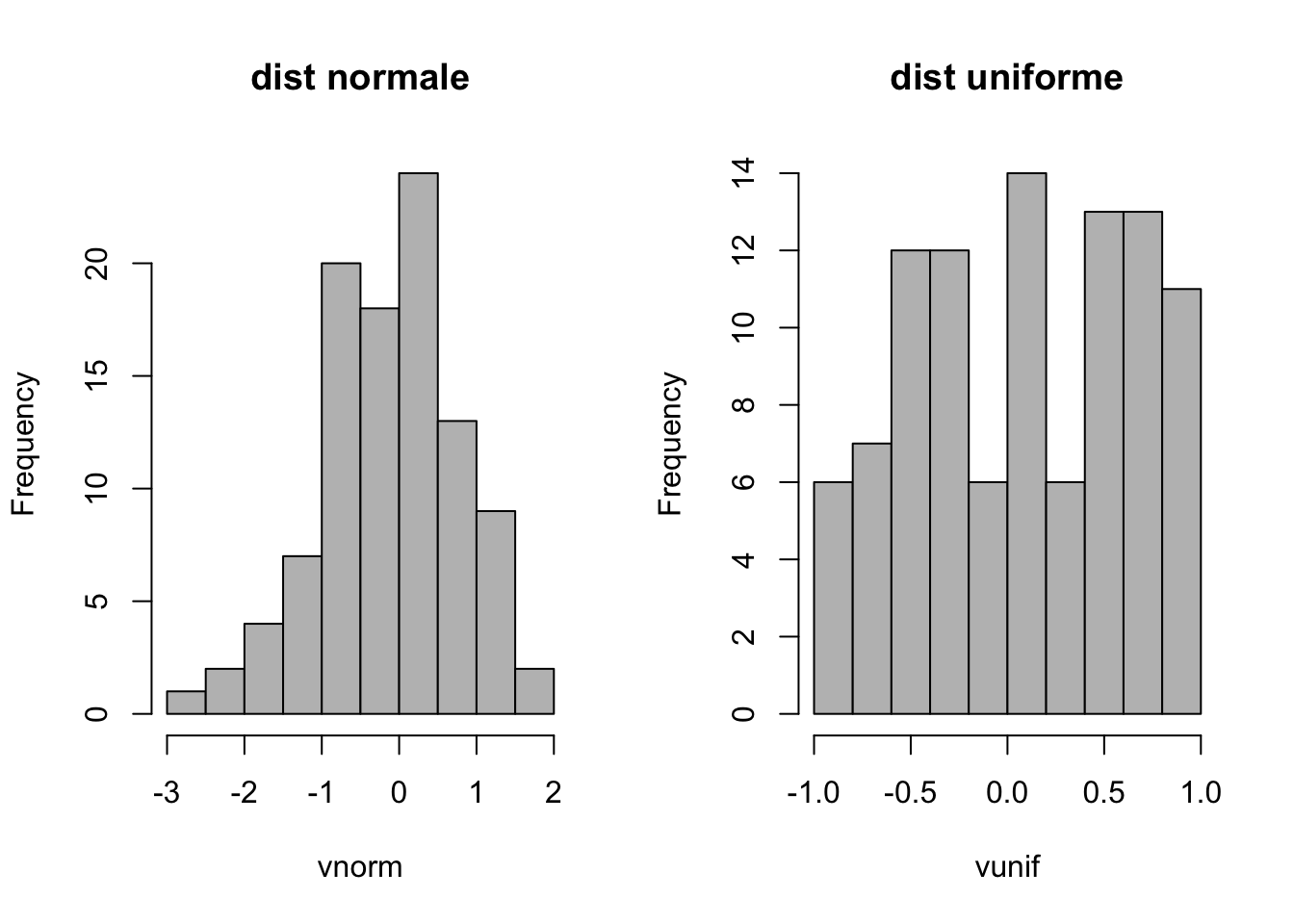
4.14.33 Leggere e scrivere (csv, file di testo, ecc.)
Ormai abbiamo imparato a fare tante cose in R con i dati, a non abbiamo ancora detto come salvarli o importarli. R sa leggere (e salvare) praticamente qualsiasi formato, inclusi quelli proprietari come xlsx o docx o pdf. Tuttavia, se R diventerà il vostro strumento preferito, vi potreste accorgere che i formati più pratici ed efficaci sono il vecchio ma intramontabile csv comma separated values o un altro formato di testo generico.
In questa introduzione alle funzione di base ci limiteremo alle funzioni per leggere/scrivere csv (read.csv e write.csv) e file di testo (read.table e write.table). Entrambe le funzioni read vogliono:
- l’argomento file che corrisponde al nome del file da caricare in R, compreso il suo percorso (se non è nella cartella di lavoro della sessione)
- l’opzione header che ci permette di dire a R se la prima riga contiene i nomi delle colonne oppure no (default)
- sep, il separatore delle colonne, che è definito per default come spazio bianco (" “) in read.table e virgola (”,") in read.csv
- dec, cioè il carattere che separa la parte intera da quella decimale dei valori numerici reali
- nel caso delle funzioni write, serve anche l’argomento x che identifica l’oggetto R che deve essere salvato nel file
R ha, comunque, un suo formato molto comodo e potente, perchè permette di salvare non solo i dati, ma anche tutte le loro caratteristiche (come la classe). I due comandi readRDS e saveRDS, molto spartani ma efficienti, vogliono al massimo (save) due argomenti:
- object cioè l’oggetto di R da salvare
- file il nome del file.
4.15 Un pò di grafici di base
Per completare la nostra parziale panoramica dei metodi base di R, è necessario esaminare le funzioni di base per produrre grafici. Queste funzioni sono estremamente flessibili e, sebbene il loro uso di base sia rapido ed efficace, possono essere utilizzate anche per produrre figure complesse.
Esistono almeno 5 tipologie di grafici di base, riassunte nella figura seguente:
gli scatterplot, cioè la rappresentazione bidimensionale di un gruppo di osservazioni (es. altezza contro peso oppure due delle 4 biometrie di iris). Questo tipo di grafico è scelta più naturale quando si vogliono esaminare correlazioni
Gli istogrammi, cioè delle rappresentazione della distribuzione dei valori di una certa variabile, tipicamente continua oppure discreta ma con tante classi ordinali. E’ la scelta più immediata quando si vuole studiare il comportamento di una certa quantità
i grafici a barre, che sono simili agli istogrammi ma generalmente sono la loro alternativa quando i dati non sono continui
i box & wisker, un vero e proprio classico per rappresentare simultaneamente varie distribuzioni di dati che, spesso, non sono normali (non seguono una distribuzione normale)
i dendrogrammi, strumento classico nella rappresentazione gerarchica di gruppi di osservazioni
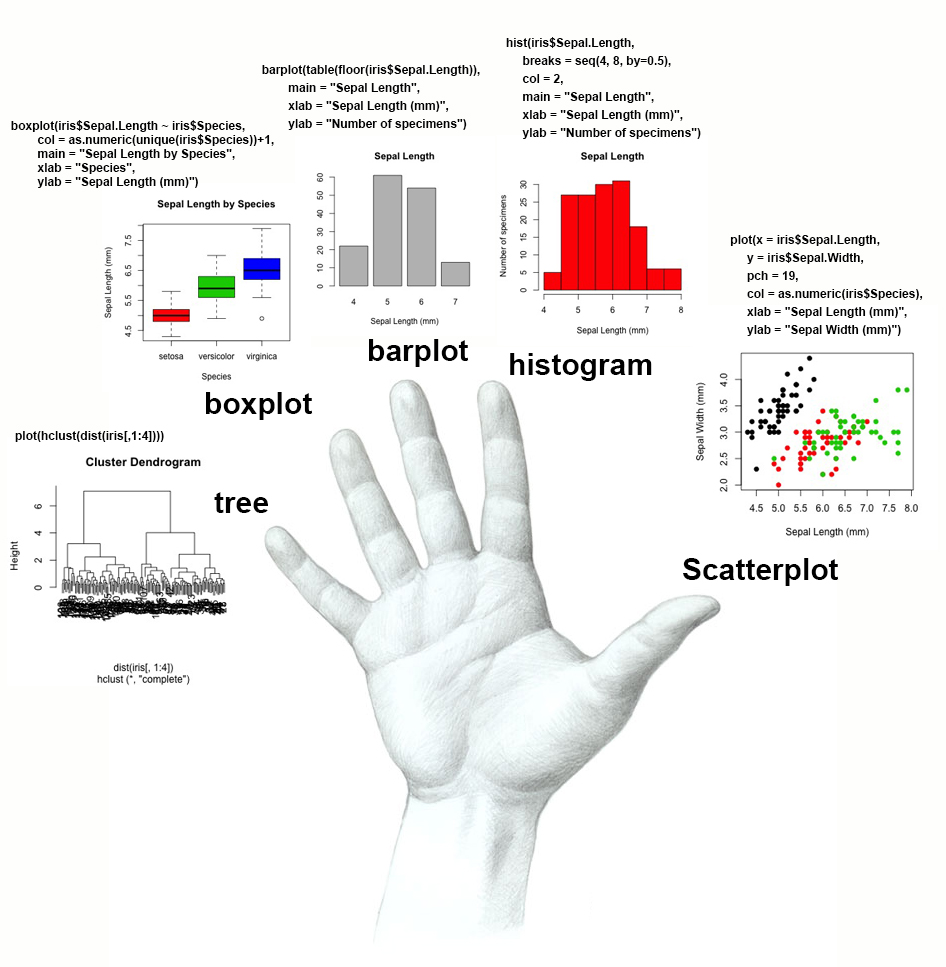
4.15.1 plot
plot è una delle funzioni più generiche di R, tanto che sarebbe più appropriato parlare di un metodo invece che di una semplice funzione. Spesso, infatti, pacchetti addizionali di R hanno delle loro specifiche funzioni plot. Questo è possibile - e avviene senza crera confusione ed equivoci tra funzioni omonime, perchè R è capace di riconoscere la classe di ogni oggetto e di applicare su di esso la funzione plot più appropriate. Vedremo tra poco come plot, se riferita a un albero di classificazione, restituisce un dendrogramma invece che uno scatterplot. Comunque, andando con ordine, cominciamo dalla funzione plot del pacchetto base, cioè appunto quella per rappresentare nuvole di punti in uno spazio bidimensionale. Gli argomenti di plot sono x (la coordinata sull’asse delle ascisse) e y (la coordinata sull’asse delle ordinate). Se le coordinate sono numerico (intere o reali non ha importanza) non c’è molto da dire, se sono dei ordinati, R li trattera come una sequenza di numeri naturali 1, 2, 3, … n dove n rappresenta il numero di livelli del factor. Se sono dei factor non ordinati… R produrra qualcosa che assomiglia a una tabella di contingenza. Vediamo degli esempi
data(iris)
iris$color = factor(rep(c("red","blue"), 75), levels = c("red","blue"))
plot(iris$Sepal.Length, iris$Sepal.Width)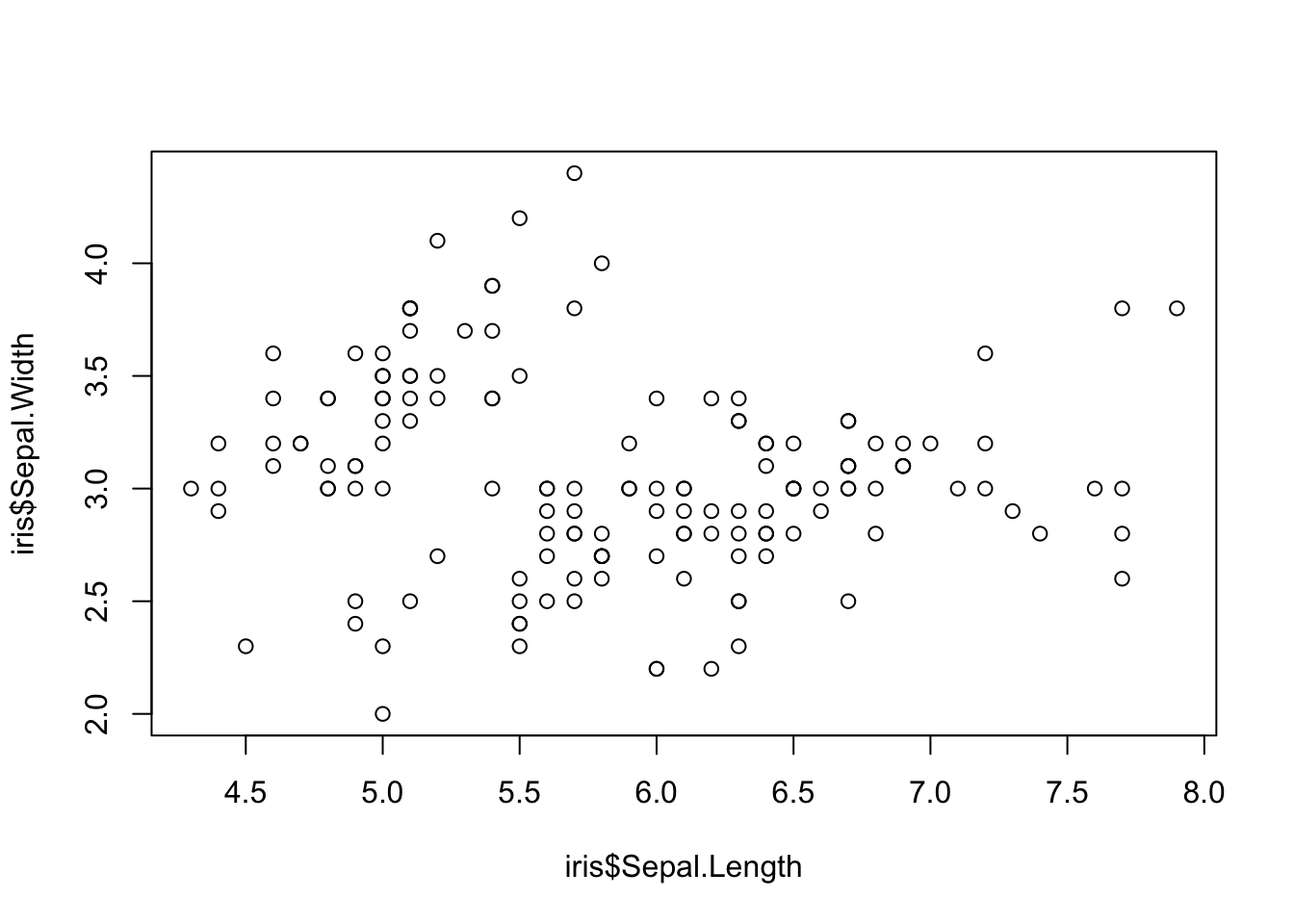
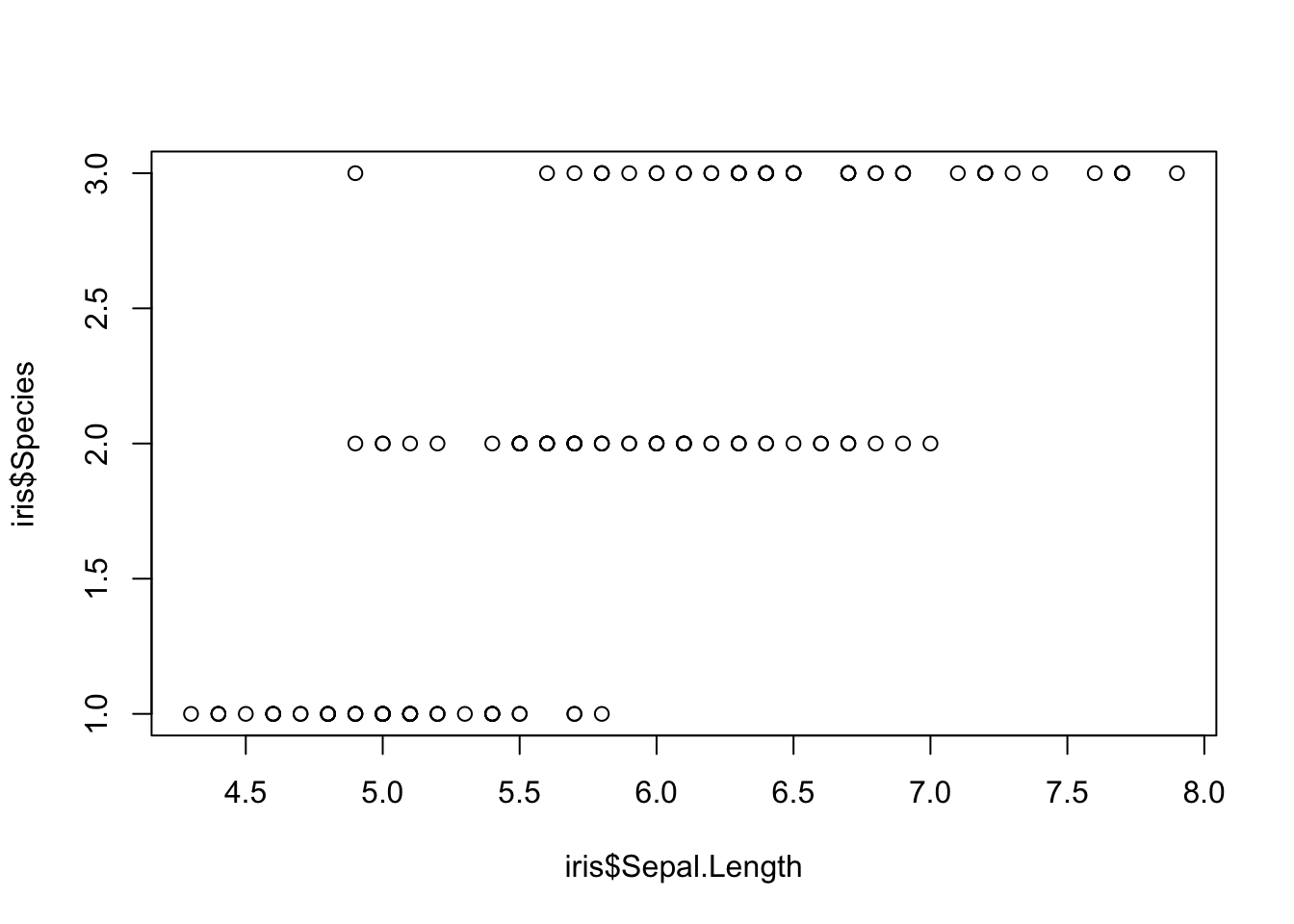
Oltre a questo, occorre solo sapere che plot ha una lunga serie di argomenti opzionali che servono a specificare:
- il tipo di grafico (punti, linee, punti e linee, etc.)
- la forma dei punti
- il colore del punti e dello sfondo
- i titoli degli assi e il titolo del grafico
- le dimesioni dei caratteri
- tanti altri aspetti (margini, ecc.)
Tutti questi argomenti opzionali sono, più propriamente, gli argomenti di un’altra funzione, chiamata par (abbraviativo di parameter) che si usa per definire questi aspetti prima di usare plot. Vediamo degli esempi
data(iris)
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19,
main = "Esempio di utilizzo dell'argomento pch")
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19, col = "red",
main = "Esempio di utilizzo dell'argomento col")
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19, col = "red", type = "b",
main = "Esempio di utilizzo dell'argomento type")
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19, col = "red", cex = 3,
main = "Esempio di utilizzo dell'argomento cex")
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19, col = "red",
xlab = "lunghezza dei sepali", ylab = "larghezza dei sepali",
main = "Esempio di utilizzo degli argomenti xlab e ylab")
par(mfrow = c(2,2))
plot(iris$Sepal.Length, iris$Sepal.Width, pch = 19)
plot(iris$Sepal.Length, iris$Petal.Length, pch = 19)
plot(iris$Sepal.Length, iris$Petal.Width, pch = 19)
plot(iris$Sepal.Width, iris$Petal.Width, pch = 19)
Nell’ultimo esempio abbiamo usato par e mfrow (un suo argomento) per inizializzare uno “spazio grafico” avente 2 righe e 2 colonne, in modo da ottenere un mosaico di scatterplot perfettamente coerenti dal punto di vista grafico (stesse proporzioni, stessi caratteri, stesso allineamento, ecc.).
Il bravo neofita è invitato a giocare con le (quasi) infinte opzioni di plot, che sarebbe noioso esaminare una per una. Piuttosto, è utile insistere sull’ “intuito” della funzione plot. Vediamo cosa succede se la applichiamo a un data frame
Il risultato è soprendente, ma non troppo: R è partito dall’assunto che il data frame sia una raccolta di osservazioni (righe) rispetto a 5 variabili… e quindi ci ha restituito uno scatterplot di tutte le possibili coppie di variabili. Un metodo rozzo ma efficace per avere una prima visione d’insieme dei dati (primo passaggio di un qualsiasi protocollo statistico di analisi dei dati).
A questo punto viene spontaneo chiedersi come si comporterà plot con oggetti di altri tipo. Vediamo degli esempi
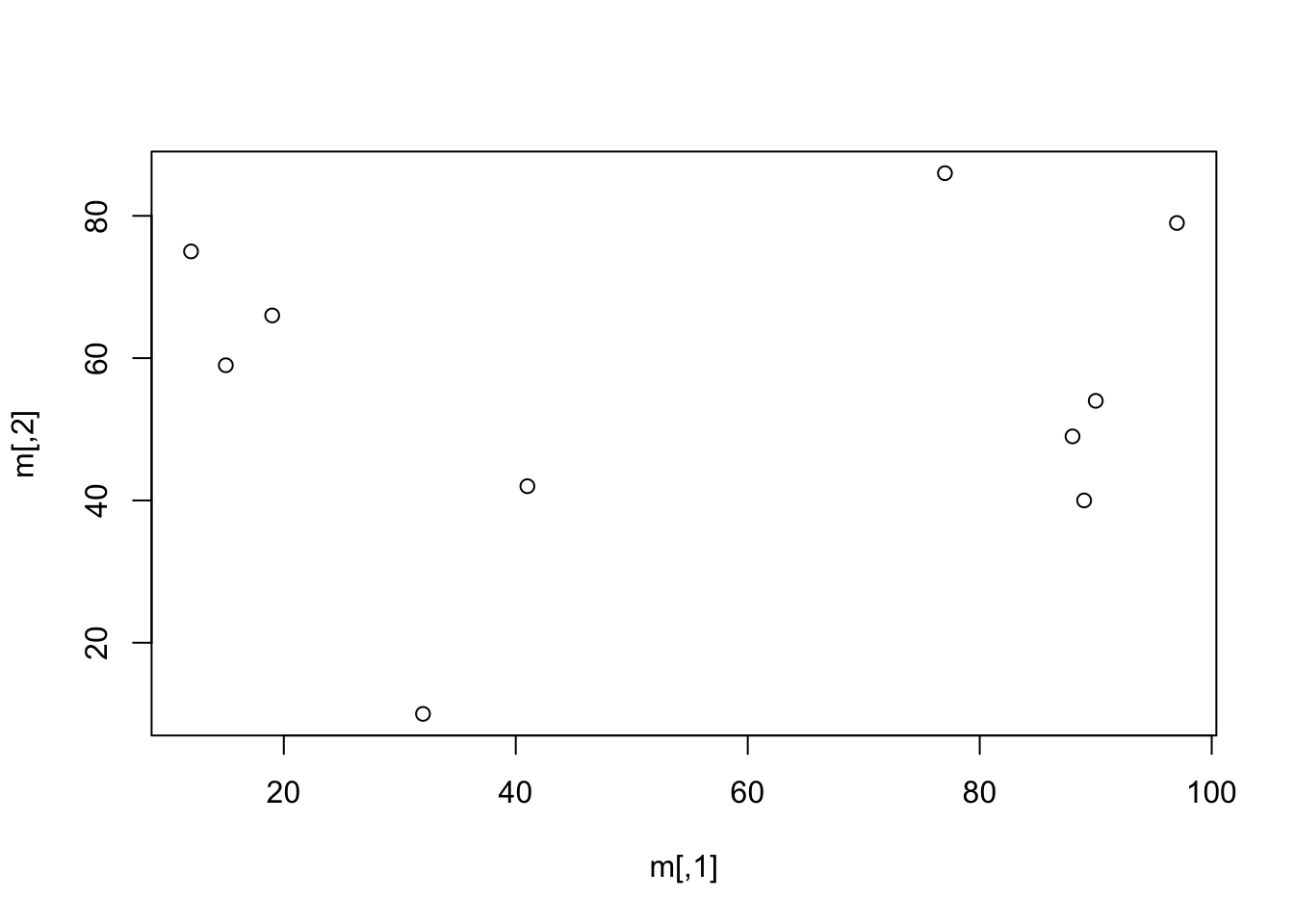
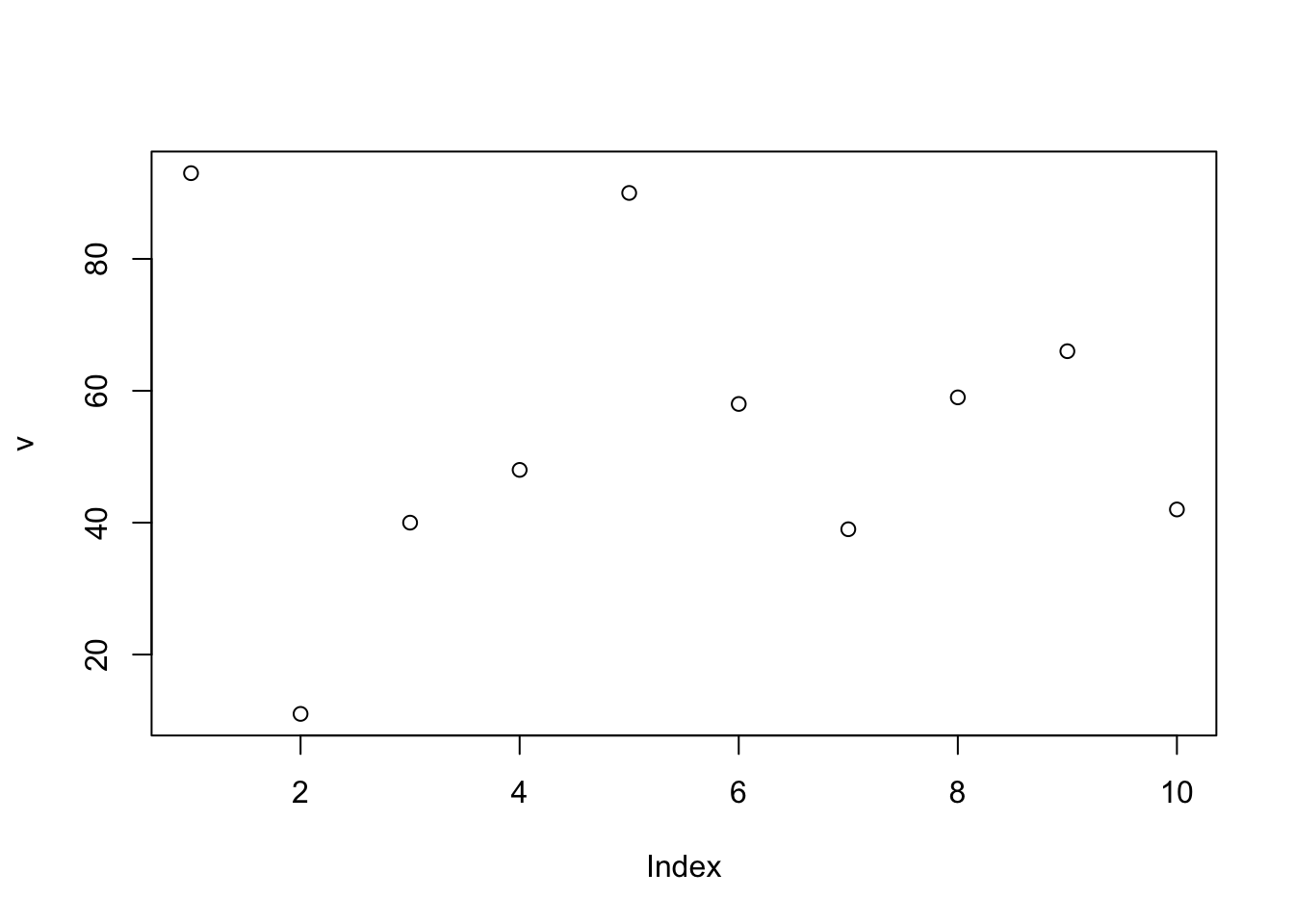
Nel primo caso (la matrice m), R ha usato le prime due colonne come x e y, rispettivamente, e ignorando la terza colonna. Ce ne accorgiamo dai nomi dei due assi dello scatterplot. Nel secondo caso (il vettore v), R ha trattato i dati come una serie e ha usato i valori del vettore come y contro una x rappresentata dagli indici di posizione degli elementi che compongono v.
4.15.2 hist
La funzione hist (da non confondere con la quasi omonimo histogram del pacchetto lattice) ha bisogno di due argomenti:
- x, cioè il vettore dei valori di cui si vuole rappresentare la distribuzione
- breaks (tagli), cioè la serie di intervalli o il criterio per generarli
Ad esempio:
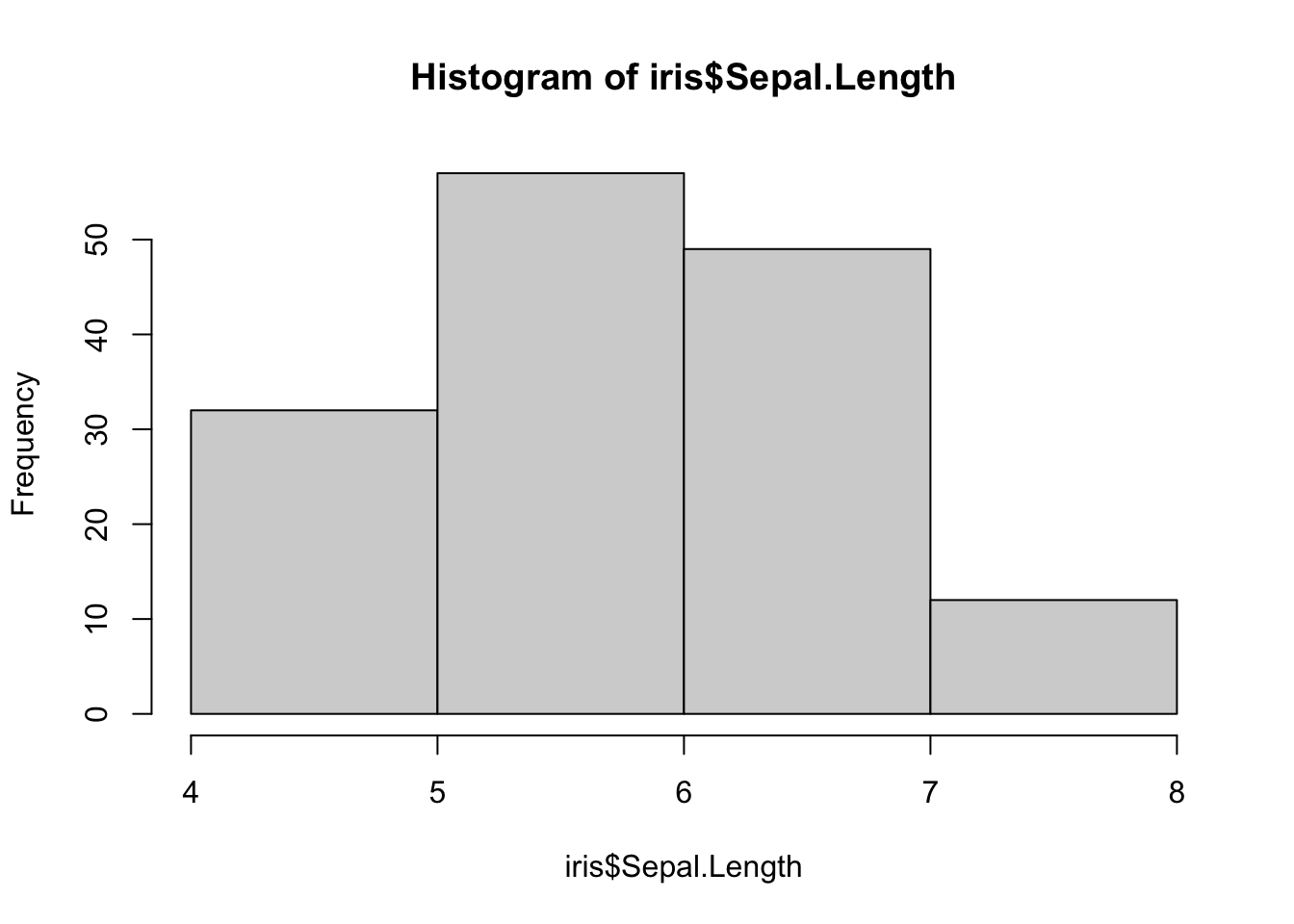
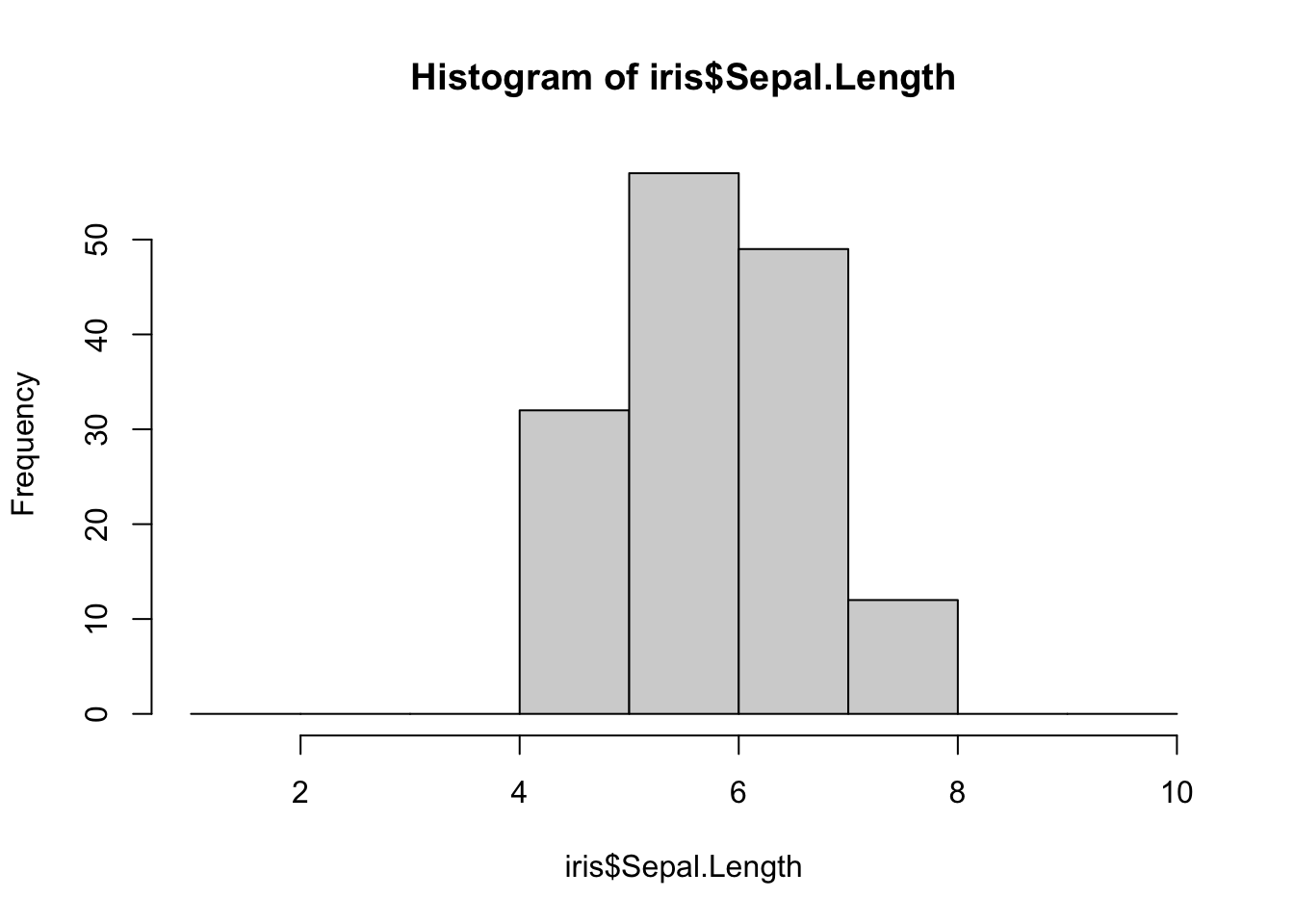
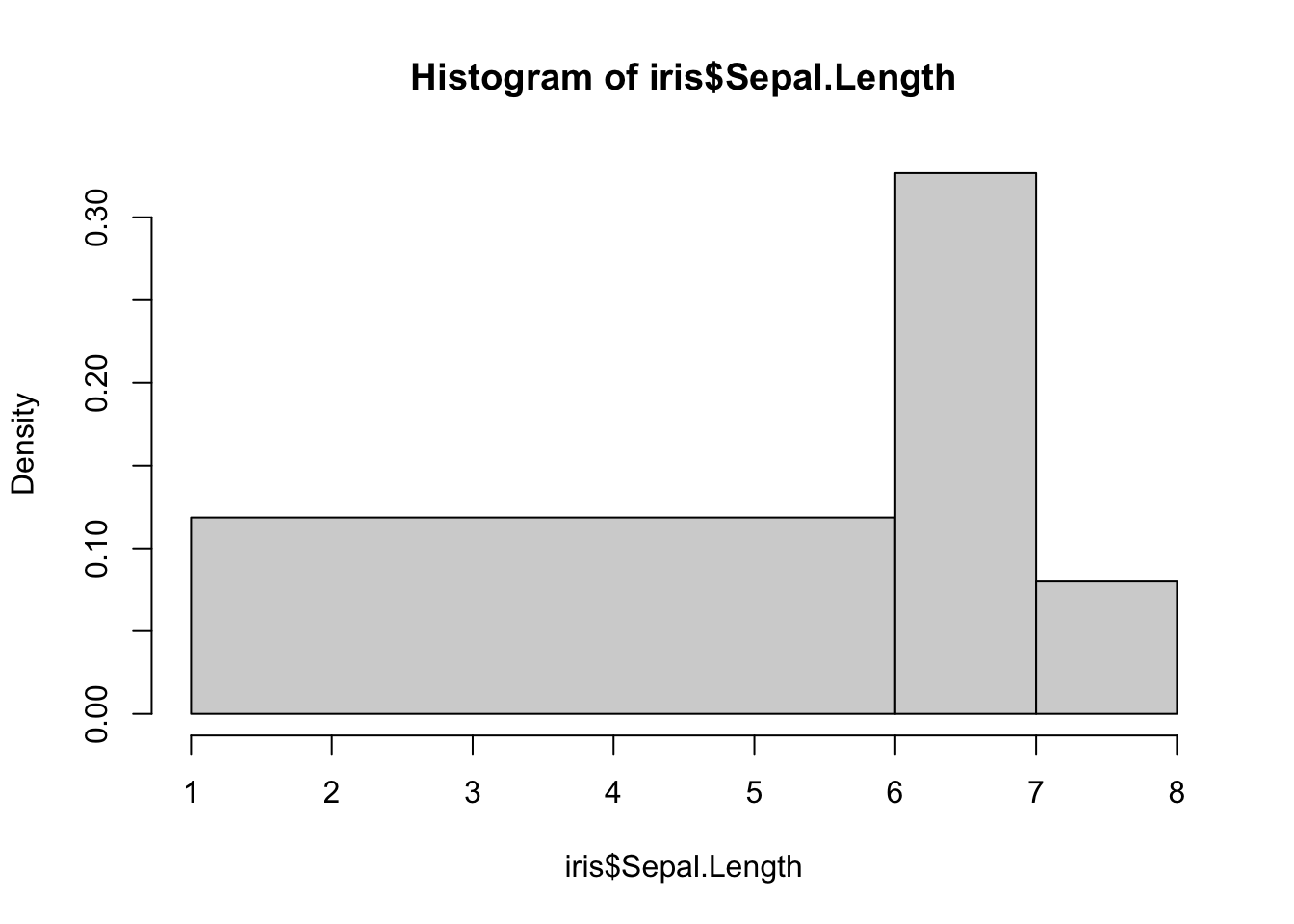
Nel primo caso abbiamo usato breaks per dire a R di fare 3 “tagli” e quindi generare 4 gruppi di dati. Nel secondo caso abbiamo specificato un vettore di intervalli omogenei. Nel terzo esempio abbiamo definito degli intervalli di ampiezza eterogenea.
Anche hist ha diverse opzioni per specificare titoli, colori, ecc.
4.15.3 barplot
Il grafico a barre è un cugino degli istogrammi ma è usato principalmente per rappresentare il numero di occorrenze rispetto a una serie di casi. Il suo unico argomento obbligatorio, height, è un vettore che rappresente appunto il numero di osservazioni, qualcosa come l’ouput della funzione table. Volendo, si possono indicare i nomi delle classi. Ad esempio:
data(iris)
iris$color = factor(sample(c("red","blue"), 150, rep = T),
levels = c("red","blue"))
tab_iris = table(iris$color)
barplot(height = tab_iris, names.arg = names(tab_iris))
Nell’esempio precedente ci siamo avvalsi della funzione names che serve a estrarre i nomi delle classi di una tabella.
4.15.4 boxplot
Il grafici del tipo Box and Wisker sono molto utili per confrontare in maniera non parametrica (cioè mediante mediana e quantili) diverse distribuzioni di dati. boxplot è una funzione molto generica, un pò come visto per plot. Vediamo alcuni esempi della sua applicazione.
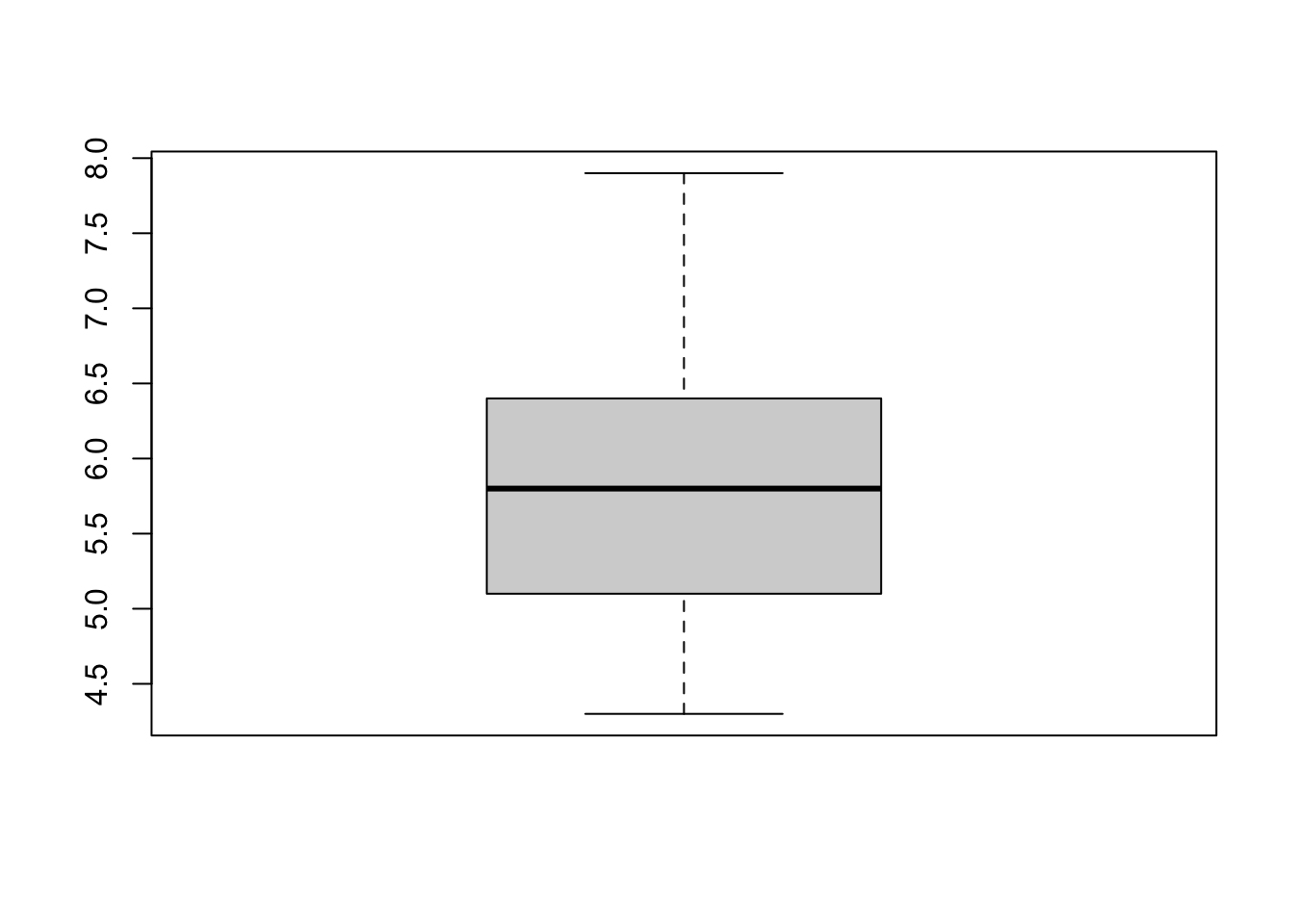
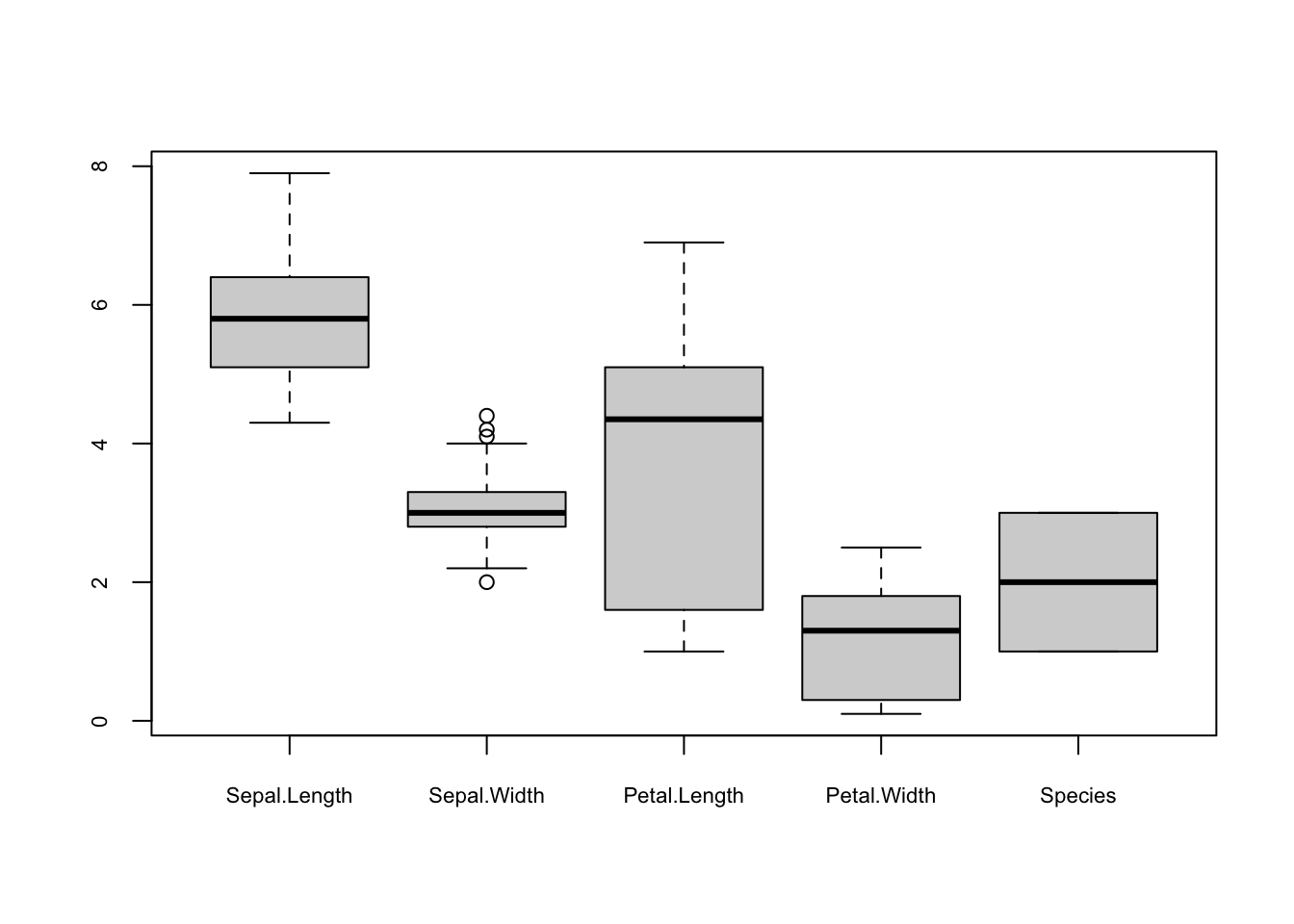
Nel primo caso abbiamo usato una singola colonna di iris e abbiamo ottenuto un singolo grafico, in cui gli estremi delle barre rappresentano il minimo e il massimo delle osservazioni, la linea nera spessa rappresenta il valore della mediana e gli estremi del rettangolo grigio rappresentano il secondo e il terzo quartile, rispettivamente. Questo genera di grafici è molto utile per catturare al volo la curtosi e la simmetria della distribuzione di una serie di valori.
Nel secondo esempio abbiamo applicato boxplot all’intero iris, ottenendo una figura per ciascuna variabile (colonna) di iris. Con la stessa logica si spiega il terzo esempio, in cui R ci restituisce le distribuzioni dei valori di ogni colonna della matrice.
Per completare il discorso su questi grafici, dobbiamo fare conoscenza con la tilde, cioè il simbolo ~ . Questo simbolo si usa, in R, per specificare una formula, cioè una relazione matematica di qualche tipo. Nel prosieguo di questo manuale la tilde diventerà di uso sempre più frequente.
Per capirne il significato, partiamo dal modello dell’equazione lineare di una retta: y = mx + q. La tilde sostituisce il simbolo = in questa formula, e ha lo stesso senso: mettere in relazione la variabile dipendente con quella(e) indipendente(i).
Adesso vediamo un suo utilizzo
L’esempio parla da solo: R ha rappresentato le distribuzioni della variabile Sepal Length rispetto alle specie, producendo un grafico molto chiaro che ci suggerisce l’esistenza di una morfologia diversa tra le diverse specie, almeno relativamente a questa singola biometria.
4.15.5 plot(2)
Anche se non abbiamo ancora introdotto le funzioni necessarie per fare analisi dei dati complesse come la cluster analysis,
Abbiamo usato due funzioni nuove, dist (che serve a calcolare una matrice di distanze) e hclust (che serve a fare le cluster analysis) per ottenere una classificazione degli individui nel data frame iris in base alle loro biometrie. Poi abbiamo applicato la funzione plot sul risultato e abbiamo ottenuto un dendrogramma. Torneremo in un altro capitolo su questo tipo di analisi statistica…
4.15.6 jpeg, bmp, png, tiff e pdf
Non ci resta che dire come fare a esportare i grafici (via via più belli) che impareremo a fare con R. Tra i tanti vantaggi di R c’è la sua capacità di produrre grafici in tanti formati e delle dimensioni e risoluzione desiderati. Tra i più comuni formati ci sono sicuramente:
il jpeg (Joint Photographic Experts Group) un comitato di esperti ISO/CCITT che ha definito il primo standard internazionale di compressione dell’immagine digitale a tono continuo, sia a livelli di grigio sia a colori, un formato molto comodo perchè leggero ma sicuramente non lo stardard ottimale per immagini di elevata qualità
il bmp (bitmap) un formato dati utilizzato per la rappresentazione di immagini raster sui sistemi operativi Microsoft Windows, uno dei formati più usati per la grafica raster
il png (Portable Network Graphics), un formato simile a quello gif ma con molte meno limitazioni
il tiff (Tagged Image File Format) è un formato immagine di tipo raster sviluppato dalla Aldus Corporation (oggi Adobe) che è molto flessibile e spesso usato per immagini di elevata qualità
Tutte queste funzioni si usano nello stesso modo per cui, dopo aver scelto il formato che più ci aggrada, dobbiamo specificare i seguenti argomenti:
- filename: il nome della figura che vogliamo generare. E’ bene darle un’estensione coerente, ad esempio .jpeg.
- width e height: la larghezza e l’altezza dell’immagine nell’unità di misura indicata da units. Può essere px (pixel), in (pollici), cm o mm.
- la sua risoluzione (res), ad esempio 120 dpi
Per applicare la funzione dobbiamo inserirla in cui codice in modo che preceda le funzioni che generano il grafico. Dopo la funzione che crea la figura, infine, è necessario specificare il comando dev(off). Questo perchè le funzioni come jpeg inizializzano un device, cioè un sottospazio in cui viene creata la figura, e per salvarla e chiudere il device è necessario appunto specificare dev(off).
Vediamo un esempio:
data(iris)
jpeg(filename = "hist.jpeg",
width = 1000, height = 600, units = "px")
hist(iris$Sepal.Length, breaks = 3)
dev.off()## quartz_off_screen
## 2Se controlliamo, la procedura ha salvato nel nostro hard disk una figura chiamata hist.jpeg contenente l’istogramma della variabile di iris Sepal.Length.